
题目列表(包括答案和解析)
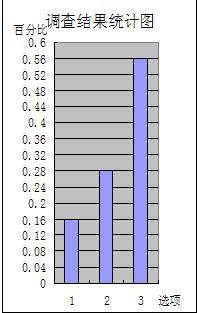 20、某路段交通拥堵现象十分严重.上周末,某同学在该路段的人行天桥处对5000名过往行人作了问卷调查:
20、某路段交通拥堵现象十分严重.上周末,某同学在该路段的人行天桥处对5000名过往行人作了问卷调查: 21、我市城市道路上的汽车与日俱增,南门天桥下的交通拥堵现象十分严重.年前,李新同学在南门天桥处对1000名过往行人做了问卷调查,问题是:从这里横过机动车通行路时,你是否自觉走人行天桥供选择的答案是:A.是;B.否;C.有时.他将得到的数据通过处理后,画出了扇形统计图,请你根据这个扇形图回答下列问题:
21、我市城市道路上的汽车与日俱增,南门天桥下的交通拥堵现象十分严重.年前,李新同学在南门天桥处对1000名过往行人做了问卷调查,问题是:从这里横过机动车通行路时,你是否自觉走人行天桥供选择的答案是:A.是;B.否;C.有时.他将得到的数据通过处理后,画出了扇形统计图,请你根据这个扇形图回答下列问题:| 1 |
| 2 |
| 1 |
| 2 |

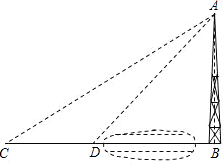 引进一个或两个中间量.以此作为媒介,再寻找这些量之间的关系,得到.于是,就可求得水塔的高,问题就解决了.
引进一个或两个中间量.以此作为媒介,再寻找这些量之间的关系,得到.于是,就可求得水塔的高,问题就解决了.| 1 |
| 3 |
| 1 |
| 2 |
| 二正 | 一正一反 | 二反 | |
| 小聪 | 24 | 50 | 26 |
| 小颖 | 24 | 47 | 29 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com