
题目列表(包括答案和解析)
|
|
|
|
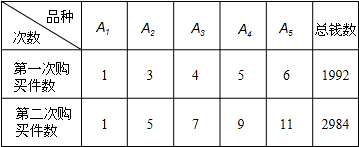
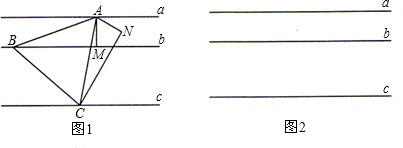
| 2 |
| 3 |
| 21 |
| 2 |
| 3 |
| 21 |
两河流交汇于点M处,甲河流水速为4km/h,乙河流水速为2km/h,一只船在静水中的速度为10km/h。某次该船只,从甲河流的上游A行驶到交汇处M后再沿乙河流逆流而上到B点,总共行驶了69km。原路返回后,发现往返所用时间相等。求此次航行往返总时间?
三、(10分)27、水平直线上顺次三点A、O、B,以O为顶点在直线上方做∠COD=40°,OM、ON分别平分∠AOC和∠BOD,求∠MON的度数。
四、(12分)28、某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时。其它主要参考数据如下:
|
运输工具 |
途中平均速度 (千米/时) |
运费 (元/千米) |
装卸费用 (元)[来源:学。科。网Z。X。X。K] |
|
火车 |
100 |
15 |
2000 |
|
汽车 |
80 |
20 |
900 |
(1) 如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答。
如果A市与某市之间的距离为S千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是A市水果批发部门的经理,要想将这种水果运往其他地区销售。你将选择哪种运输方式比较合算呢?
问题:如果存在一组平行线 ,请你猜想是否可以作等边三角形
,请你猜想是否可以作等边三角形 使其三个顶点分别在
使其三个顶点分别在 上.
上.
小明同学的解答如下:如图1所示,过点 作
作 于
于 ,作
,作 ,且
,且 ,过点
,过点 作
作 交直线
交直线 于点
于点 ,在直线
,在直线 上取点
上取点 使
使 ,则
,则 为所求.
为所求.

(1)请你参考小明的作法,在图2中作一个等腰直角三角形 使其三个顶点分别在
使其三个顶点分别在 上,点
上,点 为直角顶点;
为直角顶点;
(2)若直线 之间的距离为1,
之间的距离为1, 之间的距离为2,则在图2中,
之间的距离为2,则在图2中, ,在图1中,
,在图1中, .
.
问题:如果存在一组平行线 ,请你猜想是否可以作等边三角形
,请你猜想是否可以作等边三角形 使其三个顶点分别在
使其三个顶点分别在 上.
上.
小明同学的解答如下:如图1所示,过点 作
作 于
于 ,作
,作 ,且
,且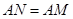 ,过点
,过点 作
作 交直线
交直线 于点
于点 ,在直线
,在直线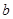 上取点
上取点 使
使 ,则
,则 为所求.
为所求.

(1)请你参考小明的作法,在图2中作一个等腰直角三角形 使其三个顶点分别在
使其三个顶点分别在 上,点
上,点 为直角顶点;
为直角顶点;
(2)若直线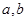 之间的距离为1,
之间的距离为1, 之间的距离为2,则在图2中,
之间的距离为2,则在图2中, ,在图1中,
,在图1中, .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com