
题目列表(包括答案和解析)
 如图,利用一面墙(墙的长度不超过45m),用79m长的篱笆围一个矩形场地,并且与墙相对留有1米宽建造一扇门方便出入(用其他材料).
如图,利用一面墙(墙的长度不超过45m),用79m长的篱笆围一个矩形场地,并且与墙相对留有1米宽建造一扇门方便出入(用其他材料).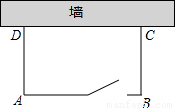
 如图,利用一面墙(墙的长度不超过45m),用79m长的篱笆围一个矩形场地,并且与墙相对留有1米宽建造一扇门方便出入(用其他材料).
如图,利用一面墙(墙的长度不超过45m),用79m长的篱笆围一个矩形场地,并且与墙相对留有1米宽建造一扇门方便出入(用其他材料).
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com