
题目列表(包括答案和解析)
 门票为每张x元,且40≤x≤70,经市场调研发现一天游览人数y与票价x之间存在着如图所示的一次函数关系.
门票为每张x元,且40≤x≤70,经市场调研发现一天游览人数y与票价x之间存在着如图所示的一次函数关系.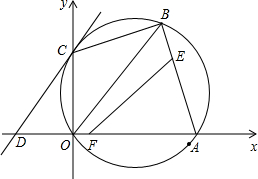 (2009•北仑区模拟)如图,在平面直角坐标系中,△OAB的外接圆交y轴于点C,已知点A的坐标(12,0),点B的坐标(
(2009•北仑区模拟)如图,在平面直角坐标系中,△OAB的外接圆交y轴于点C,已知点A的坐标(12,0),点B的坐标(| 600 |
| 169 |
| 1440 |
| 169 |
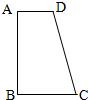 18、已知:直角梯形ABCD中,AD∥BC,∠B为直角.
18、已知:直角梯形ABCD中,AD∥BC,∠B为直角.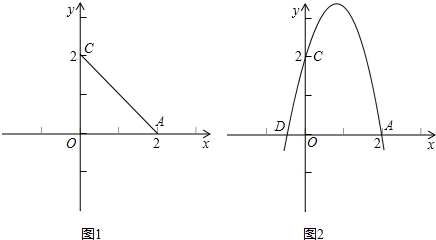
| 1 | 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com