
题目列表(包括答案和解析)
| 8 |
| x |
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 14 | 7 | 5.34 | 5.11 | 5.01 | 5 | 5.01 | 5.04 | 5.08 | 5.67 | 7 | 8.6 | 12.14 | … |
| 8 |
| x |
| 8 |
| x |
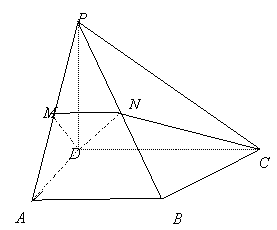 如图,四棱锥P-ABCD中,PD
如图,四棱锥P-ABCD中,PD![]() 底面ABCD,AD
底面ABCD,AD![]() AB,CD//AB且AB=
AB,CD//AB且AB=![]() AD,PA与底面ABCD成60
AD,PA与底面ABCD成60![]() 角,点M,N分别是PA,PB的中点.
角,点M,N分别是PA,PB的中点.
(Ⅰ)求证:AB![]() 平面PAD;
平面PAD;
(Ⅱ)求二面角P-MN-D的大小;
(Ⅲ)当![]() 为何值时,DN
为何值时,DN![]() BC,并请证明你的结论.
BC,并请证明你的结论.




一.选择题:
题号
1
2
3
4
5
6
7
8
答案
C
A
C
B
B
A
B
D
二.填空题:
9.6、30、10;
10.?5;
11..files/image211.gif) ;
;
12.?250;
13..files/image213.gif) ;
14.③④
;
14.③④
三.解答题:
15.解: .files/image215.gif) ; ………5分
; ………5分
.files/image217.gif) 方程
方程.files/image219.gif) 有非正实数根
有非正实数根.files/image221.gif)
.files/image223.gif)
综上:.files/image225.gif) ……………………12分16.解:(I)设袋中原有
……………………12分16.解:(I)设袋中原有.files/image204.gif) 个白球,由题意知
个白球,由题意知.files/image228.gif)
可得.files/image230.gif) 或
或.files/image232.gif) (舍去)
(舍去)
答:袋中原有3个白球. 。。。。。。。。4分
(II)由题意,.files/image100.gif) 的可能取值为1,2,3,4,5
的可能取值为1,2,3,4,5
.files/image235.gif)
.files/image237.gif)
.files/image239.gif)
.files/image241.gif)
所以.files/image100.gif) 的分布列为:
的分布列为:
.files/image100.gif)
1
2
3
4
5
.files/image245.gif)
.files/image247.gif)
.files/image249.gif)
.files/image251.gif)
.files/image253.gif)
.files/image255.gif)
。。。。。。。。。9分
(III)因为甲先取,所以甲只有可能在第一次,第三次和第5次取球,记”甲取到白球”为事件.files/image257.gif) ,则
,则.files/image259.gif)
答:甲取到白球的概率为.files/image261.gif) .。。。。。。。。13分
.。。。。。。。。13分
17.解:(1)由.files/image060.gif) =
=.files/image264.gif) .
..files/image266.gif) =
=.files/image268.gif) ,∴
,∴.files/image109.gif) =1;。。。。。。。。。4分
=1;。。。。。。。。。4分
(2)任取.files/image271.gif) 、
、.files/image273.gif) ∈(1,+∞),且设
∈(1,+∞),且设.files/image271.gif) <
<.files/image273.gif) ,则:
,则:
.files/image277.gif) -
-.files/image279.gif) =
=.files/image281.gif) >0,
>0,
∴.files/image060.gif) =
=.files/image284.gif) 在(1,+∞)上是单调递减函数;。。。。。。。。。8分
在(1,+∞)上是单调递减函数;。。。。。。。。。8分
(3)当直线.files/image107.gif) =
=.files/image096.gif) (
(.files/image096.gif) ∈R)与
∈R)与.files/image060.gif) 的图象无公共点时,
的图象无公共点时,.files/image096.gif) =1,
=1,
∴.files/image115.gif) <2+
<2+.files/image290.gif) =4=
=4=.files/image292.gif) ,|
,|.files/image119.gif) -2|+
-2|+.files/image295.gif) >2,
>2,
得:.files/image119.gif) >
>.files/image297.gif) 或
或.files/image119.gif) <
<.files/image295.gif) .。。。。。。。。13分
.。。。。。。。。13分
18.(Ⅰ)证明:∵.files/image131.gif) 底面
底面.files/image133.gif) ,
,.files/image301.gif) 底面
底面.files/image133.gif) , ∴
, ∴.files/image303.gif)
又∵.files/image305.gif) 且
且.files/image307.gif) 平面
平面.files/image150.gif) ,
,.files/image307.gif) 平面
平面.files/image150.gif) ,
,.files/image310.gif) ,
,
∴.files/image148.gif) 平面
平面.files/image150.gif) ;
;.files/image314.gif) 3分
3分
.files/image323.gif) (Ⅱ)解:∵点
(Ⅱ)解:∵点.files/image144.gif) 分别是
分别是.files/image146.gif) 的中点,
的中点,
∴.files/image327.gif) ,由(Ⅰ)知
,由(Ⅰ)知.files/image148.gif) 平面
平面.files/image150.gif) ,
,
∴.files/image329.gif) 平面
平面.files/image150.gif) ,
,
∴.files/image329.gif)
.files/image331.gif) ,
,.files/image329.gif)
.files/image333.gif) ,
,
∴.files/image335.gif) 为二面角
为二面角.files/image152.gif) 的平面角,
的平面角,
∵.files/image131.gif) 底面
底面.files/image133.gif) ,∴
,∴.files/image139.gif) 与底面
与底面.files/image133.gif) 所成的角即为
所成的角即为.files/image340.gif) ,
,
∴.files/image340.gif) =
=.files/image142.gif) ,∵
,∵.files/image343.gif) 为直角三角形斜边的中点,
为直角三角形斜边的中点,
∴.files/image345.gif) 为等腰三角形,且
为等腰三角形,且.files/image347.gif) ,∴
,∴.files/image335.gif)
.files/image350.gif) ;
;
(Ⅲ)过点.files/image352.gif) 作
作.files/image354.gif) 交
交.files/image356.gif) 于点
于点.files/image358.gif) ,∵
,∵.files/image131.gif) 底面
底面.files/image133.gif) ,
,
∴.files/image360.gif) 底面
底面.files/image133.gif) ,
,.files/image356.gif) 为直线
为直线.files/image363.gif) 在底面
在底面.files/image133.gif) 上的射影,
上的射影,
要.files/image156.gif) ,由三垂线定理的逆定理有要
,由三垂线定理的逆定理有要 .files/image366.gif) ,
,
设.files/image368.gif) ,则由
,则由.files/image137.gif) 得
得.files/image371.gif) ,
,
又.files/image305.gif) ∴在直角三角形
∴在直角三角形.files/image374.gif) 中,
中,.files/image376.gif) ,
,
∴.files/image378.gif)
.files/image380.gif) ,
,
∵ .files/image382.gif) ∴
∴.files/image384.gif) ,
,.files/image378.gif)
.files/image386.gif)
.files/image388.gif) ,
,
在直角三角形.files/image390.gif) 中,
中,.files/image392.gif) ,
,
.files/image398.gif)
.files/image400.gif) ,即
,即.files/image402.gif) 时,
时,.files/image156.gif) .
.
(Ⅲ)以点.files/image405.gif) 为坐标原点,建立如图的直角坐标系,设
为坐标原点,建立如图的直角坐标系,设.files/image407.gif) ,则
,则.files/image409.gif) ,
,.files/image411.gif) ,设
,设.files/image413.gif) ,则
,则.files/image415.gif)
则.files/image417.gif) ,
,.files/image419.gif) ,
,.files/image421.gif) ,
,
.files/image423.gif) ,时
,时.files/image425.gif)
.files/image427.gif) 时,
时,.files/image429.gif)
.files/image431.gif) .
.
有 .files/image435.gif) =
=.files/image437.gif) =
=.files/image439.gif) ……(3分)
……(3分)
∴当.files/image441.gif) 时,
时,.files/image443.gif) ,即
,即.files/image445.gif)
当.files/image441.gif) 时,函数f(x)是凸函数. ……(4分)
时,函数f(x)是凸函数. ……(4分)
(2) 当x=0时, 对于a∈R,有f(x)≤1恒成立;当x∈(0, 1]时, 要f(x)≤1恒成立
即.files/image448.gif) , ∴
, ∴ .files/image450.gif) 恒成立,∵ x∈(0, 1], ∴
恒成立,∵ x∈(0, 1], ∴ .files/image452.gif) ≥1, 当
≥1, 当.files/image452.gif) =1时,
=1时, .files/image454.gif) 取到最小值为0,∴ a≤0, 又a≠0,∴ a的取值范围是
取到最小值为0,∴ a≤0, 又a≠0,∴ a的取值范围是.files/image456.gif) .
.
由此可知,满足条件的实数a的取值恒为负数,由(1)可知函数f(x)是凸函数………10分
(3)令.files/image458.gif) 则
则.files/image460.gif) ,∵
,∵.files/image181.gif) ,∴
,∴.files/image463.gif) ,……………..(11)分
,……………..(11)分
令.files/image465.gif) ,则
,则.files/image467.gif) ,故
,故.files/image469.gif) ;
;
若.files/image471.gif) ,则
,则 .files/image473.gif)
.files/image475.gif) ;,……………..(12)分
;,……………..(12)分
若.files/image477.gif) ,则
,则.files/image479.gif) ∴
∴.files/image481.gif) ;∴
;∴.files/image483.gif) 时,
时,.files/image485.gif) .
.
综上所述,对任意的.files/image483.gif) ,都有
,都有.files/image485.gif) ;……………..(13)分
;……………..(13)分
.files/image489.gif) 所以,
所以,.files/image060.gif) 不是R上的凸函数. ……………..(14)分
不是R上的凸函数. ……………..(14)分
对任意.files/image492.gif) ,有
,有.files/image494.gif)
.files/image496.gif) ,
,
所以,.files/image060.gif) 不是
不是.files/image172.gif) 上的凸函数. ……………..(14)分
上的凸函数. ……………..(14)分
20. 解:(1).files/image499.gif) 设数列
设数列.files/image200.gif) 的前
的前.files/image204.gif) 项和为
项和为.files/image503.gif) ,则
,则.files/image505.gif)
.files/image507.gif)
.files/image509.gif)
.files/image193.gif) ……….4分
……….4分
(2).files/image204.gif) 为偶数时,
为偶数时,.files/image513.gif)
.files/image204.gif) 为奇数时,
为奇数时,.files/image515.gif)
.files/image517.gif)
.files/image193.gif) ………9分
………9分
(3)方法1、因为.files/image519.gif) 所以
所以.files/image521.gif)
当.files/image523.gif) ,时,
,时,.files/image525.gif) ,
,.files/image527.gif) 时
时.files/image529.gif)
又由.files/image519.gif)
.files/image531.gif) ,两式相减得
,两式相减得
.files/image533.gif)
.files/image535.gif) 所以若
所以若.files/image206.gif)
.files/image193.gif) ,则有
,则有.files/image209.gif) ………..14分
………..14分
方法2、由.files/image519.gif)
.files/image531.gif) ,两式相减得
,两式相减得
.files/image533.gif)
.files/image535.gif) ………..11分
………..11分
所以要证明.files/image209.gif) ,只要证明
,只要证明.files/image539.gif)
或①由:.files/image541.gif)
所以.files/image543.gif) …………………14分
…………………14分
或②由:.files/image545.gif)
.files/image547.gif)
.files/image549.gif) …………………14分
…………………14分
数学归纳法:①当.files/image551.gif)
当.files/image553.gif)
②当.files/image555.gif)
当.files/image557.gif)
综上①②知若.files/image206.gif)
.files/image193.gif) ,则有
,则有.files/image559.gif) .
.
所以,若.files/image206.gif)
.files/image193.gif) ,则有
,则有.files/image209.gif) .。。。。。。。。。14分
.。。。。。。。。。14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com