练习册

  • 练习册
  • 试题
    高三数学理科答卷 【查看更多】

     

    题目列表(包括答案和解析)

    某校高三数学理科组有10名教师，其中4名女老师；文科组有5位老师，其中3位女老师．现在采取分层抽样的方法（层内采用不放回简单随机抽样）从文、理两科中抽取3名教师进行“标、纲、题”测试．
    （1）求从文、理两科各抽取的人数．
    （2）求从理科组抽取的教师中恰有1名女教师的概率．
    （3）记ξ表示抽取的3名教师中男教师人数，求ξ的概率分布列及数学期望．

    查看答案和解析>>

    某校高三数学理科组有10名教师，其中4名女老师；文科组有5位老师，其中3位女老师．现在采取分层抽样的方法（层内采用不放回简单随机抽样）从文、理两科中抽取3名教师进行“标、纲、题”测试．
    （1）求从文、理两科各抽取的人数．
    （2）求从理科组抽取的教师中恰有1名女教师的概率．
    （3）记ξ表示抽取的3名教师中男教师人数，求ξ的概率分布列及数学期望．

    查看答案和解析>>

    某校高三数学理科组有10名教师，其中4名女老师；文科组有5位老师，其中3位女老师．现在采取分层抽样的方法（层内采用不放回简单随机抽样）从文、理两科中抽取3名教师进行“标、纲、题”测试．
    （1）求从文、理两科各抽取的人数．
    （2）求从理科组抽取的教师中恰有1名女教师的概率．
    （3）记ξ表示抽取的3名教师中男教师人数，求ξ的概率分布列及数学期望．

    查看答案和解析>>

    实数x、y满足不等式组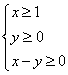，则W=的取值范围（ 　 ）

    A．[－1,0]　　 B．(－∞,0]　　 C．[－1,+∞)　　 D．[－1,1)

    高三数学理科（A）第三次月考试卷　 第1页　　 共8页　　　　　　　　　　　　　　 高三数学理科（A）第三次月考试卷　 第2页　　 共8页　

    查看答案和解析>>

    某校从参加高三年级理科综合物理考试的学生中随机抽出名学生，将其数学成绩（均为整数）分成六段，…后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：

    （Ⅰ）求分数在内的频率，并补全这个频率分布直方图；

    （Ⅱ）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的

    平均分；

    （Ⅲ）若从名学生中随机抽取人，抽到的学生成绩在记分，在记分，

    在记分，用表示抽取结束后的总记分，求的分布列和数学期望.

    【解析】（1）中利用直方图中面积和为1，可以求解得到分数在内的频率为

    （2）中结合平均值可以得到平均分为：

    （3）中用表示抽取结束后的总记分x, 学生成绩在的有人，在的有人，在的有人,结合古典概型的概率公式求解得到。

    (Ⅰ)设分数在内的频率为，根据频率分布直方图，则有，可得，所以频率分布直方图如右图.……4分

    （求解频率3分，画图1分）

    （Ⅱ）平均分为：……7分

    （Ⅲ）学生成绩在的有人，在的有人，

    在的有人.并且的可能取值是.    ………8分

    则；； ；

    ；.（每个1分）

    所以的分布列为

    0

    1

    2

    3

    4

    …………………13分

     

    查看答案和解析>>

    1――12   A  B  B  B  B  C  D  D  C  A  C  B

     

    13、1            14、e             15、      16、①②④     

    17、解在上是增函数，

    方程=x2 + (m ? 2 )x + 1 = 0的两个根在0至3之间

    ∴∴∴＜m≤0

    依题意得：m的取值范围是:＜m≤-1或m＞0

    18、解：（1）,

    当a=1时　解集为

    当a>1时，解集为，

    当0<a<1时，解集为；

    （2）依题意知f(1)是f(x)的最小值，又f(1)不可能是端点值，则f(1)是f(x)的一个极小值，由，

    19、解：（1）当所以f(-x)＝-(-x)2-(-x)+5=-x2+x+5，

     

    所以f(x)=

    （2）由题意，不妨设Ａ点在第一象限，坐标为(t,-t2-t+5)其中，，

    则S(t)=S ABCD=2t(-t2-t+5)=-2t3-2t2+10t.，

    令得（舍去），t2=1.

    当时，所以S(t)在上单调递增，在上单调递减，

    所以当t=1时，ABCD的面积取得极大值也是S(t)在上的最大值。

    从而当t=1时，矩形ABCD的面积取得最大值6.

    20、解：

    21、解：，

    令，要使在其定义域内为单调函数，只需在内满足：或恒成立.

    ① 当时，，∵，∴，∴，

    ∴在内为单调递减.  

    ② 当时，，对称轴为， ∴.

    只需，即时，，

    ∴在内为单调递增。

     ③当时，，对称轴为.

    只需，即时在恒成立.

    综上可得，或.     

    22、解：（Ⅰ）

           

            同理，令

            ∴f(x)单调递增区间为，单调递减区间为.

            由此可知

       （Ⅱ）由（I）可知当时，有，

            即.

        .

      （Ⅲ） 设函数

           

            ∴函数）上单调递增，在上单调递减.

            ∴的最小值为，即总有

            而

           

            即

            令则

           

           

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     


    同步练习册答案