题目列表(包括答案和解析)
（本题满分12分）
对甲、乙两种商品的重量的误差进行抽查，测得数据如下(单位：
)：
甲：13 15 14 14 9 14 21 9 10 11
乙：10 14 9 12 15 14 11 19 22 16
（1）画出样本数据的茎叶图，并指出甲，乙两种商品重量误差的中位数；
（2）计算甲种商品重量误差的样本方差；
（3）现从重量误差不低于15的乙种商品中随机抽取两件，求重量误差为19的商品被抽
中的概率。
（本题满分12分）设{an}是等差数列，{bn}是各项都为正数的等比数列，且a1=b1=1，a3+b5=21，a5+b3=13.
(1)求{an}，{bn}的通项公式；
(2)求数列
的前n项和Sn.
（本题满分12分）
对甲、乙两种商品的重量的误差进行抽查，测得数据如下(单位：
)：
甲：13 15 14 14 9 14 21 9 10 11
乙：10 14 9 12 15 14 11 19 22 16
（1）画出样本数据的茎叶图，并指出甲，乙两种商品重量误差的中位数；
（2）计算甲种商品重量误差的样本方差；
（3）现从重量误差不低于15的乙种商品中随机抽取两件，求重量误差为19的商品被抽
中的概率。
（本题满分12分）探究函数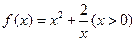
的最小值，并确定取得最小值时x的值. 列表如下, 请观察表中y值随x值变化的特点，完成以下的问题.
| x | … | 0.25 | 0.5 | 0.75 | 1 | 1.1 | 1.2 | 1.5 | 2 | 3 | 5 | … |
| y | … | 8.063 | 4.25 | 3.229 | 3 | 3.028 | 3.081 | 3.583 | 5 | 9.667 | 25.4 | … |
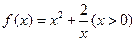在区间（0，1）上递减，问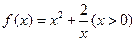：在区间 上递增.当
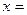时，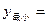
；
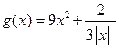在定义域内有最大值或最小值吗？如有，是多少？此时x为何值？（直接回答结果，不需证明）（本题满分12分）对甲、乙两种商品的重量的误差进行抽查，测得数据如下(单位：
)：
甲：13 15 14 14 9 14 21 9 10 11
乙：10 14 9 12 15 14 11 19 22 16
（1）画出样本数据的茎叶图，并指出甲，乙两种商品重量误差的中位数；
（2）计算甲种商品重量误差的样本方差；
（3）现从重量误差不低于15的乙种商品中随机抽取两件，求重量误差为19的商品被抽中的概率。
1――12 A B B B B C D D C A C B
13、1 14、e 15、
16、①②④
17、解
在
上是增函数，
方程
=x2 + (m ? 2 )x + 1 = 0的两个根在0至3之间
∴
∴
∴
＜m≤0
依题意得：m的取值范围是:＜m≤-1或m＞0
18、解：（1）
,
当a=1时 解集为
当a>1时，解集为
，
当0<a<1时，解集为
；
（2）依题意知f(1)是f(x)的最小值，又f(1)不可能是端点值，则f(1)是f(x)的一个极小值，由
，
19、解：（1）当
所以f(-x)＝-(-x)2-(-x)+5=-x2+x+5，
所以f(x)=
（2）由题意，不妨设Ａ点在第一象限，坐标为(t,-t2-t+5)其中，
，
则S(t)=S ABCD=2t(-t2-t+5)=-2t3-2t2+10t.
，
令
得
（舍去），t2=1.
当
时
，所以S(t)在
上单调递增，在
上单调递减，
所以当t=1时，ABCD的面积取得极大值也是S(t)在上的最大值。
从而当t=1时，矩形ABCD的面积取得最大值6.
20、解：
21、解：
，
令
，要使
在其定义域内为单调函数，只需
在内满足：
或
恒成立.
① 当
时，
，∵
，∴
，∴
，
∴在内为单调递减.
② 当
时，，对称轴为
， ∴
.
只需
，即
时，
，
∴在内为单调递增。
③当
时，，对称轴为
.
只需
，即
时在恒成立.
综上可得，或.
22、解：（Ⅰ）
同理，令
∴f(x)单调递增区间为
，单调递减区间为
.
由此可知
（Ⅱ）由（I）可知当
时，有
，
即
.
.
（Ⅲ） 设函数
∴函数
）上单调递增，在
上单调递减.
∴的最小值为
，即总有
而
即
令
则
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com