题目列表(包括答案和解析)
本题有(1)．(2)．(3)三个选做题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
（1）(本小题满分7分)选修4－2：矩阵与变换选做题
已知矩阵A=
有一个属于特征值1的特征向量
.
(Ⅰ) 求矩阵A；
(Ⅱ) 矩阵B=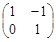
，点O(0,0)，M(2，-1)，N(0，2)，求
在矩阵AB的对应变换作用下所得到的
的面积.
（2）(本小题满分7分)选修4－4：坐标系与参数方程选做题
在直角坐标平面内，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系.已知曲线
的参数方程为
，曲线
的极坐标方程为
．
（Ⅰ）将曲线的参数方程化为普通方程；（Ⅱ）判断曲线与曲线的交点个数，并说明理由．
（3）(本小题满分7分)选修4－5：不等式选讲选做题
已知函数
，不等式
在
上恒成立．
（Ⅰ）求
的取值范围；
（Ⅱ）记的最大值为
，若正实数
满足
，求
的最大值．
（A）将圆M：x2＋y2＝a（a＞0）的横坐标伸长为原来的2倍，纵坐标缩短为原来的
，正好与直线x－y＝1相切，若以原点为极点，x轴非负半轴为极轴建立极坐标系，则圆M的极坐标方程为
（B）关于x的不等式：2－x2＞|x－a|至少有一个负数解，则实数a的取值范围是
，正好与直线x－y＝1相切，若以原点为极点，x轴非负半轴为极轴建立极坐标系，则圆M的极坐标方程为 一、选择题
题号
1
2
3
4
5
6
7
8
答案
A
C
B
D
A
B
A
B
1. A∵
∴
即
， 
，
∴
故选A；
C 
3 B 
4. D．由奇函数
可知
，而
，则
，当
时，
；当
时，
，又在
上为增函数，则奇函数在
上为增函数，
.
5 A 如图知
是斜边为3 的等腰直角三角形，
是直角边为1等腰直角三角形，区域的面积
6. B 
，而
所以
，得
7. A 
，即
8. B
，所以解集为
，
又
，因此选B。
二、填空题
9. （－
，1）. 10. 
. 11. 
12. 
13. 
.
14. 
.
9. 
，
，
∴点M的直角坐标为（－，1）。
10.
11. 联立解方程组
解得
，
即两曲线的交点为
12. . ∴
，
13. . 
14. .依题意得
所以
，
三、解答题
15解：解法1：设矩形栏目的高为a cm，宽为b cm，则ab=9000. ①
广告的高为a+20，宽为2b+25，其中a＞0，b＞0.
广告的面积S＝(a+20)(2b+25)
＝2ab+40b+25a+500＝18500+25a+40b
≥18500+2
=18500+
当且仅当25a＝40b时等号成立，此时b=
,代入①式得a=120，从而b=75.
即当a=120，b=75时,S取得最小值24500.
故广告的高为140 cm,宽为175 cm时，可使广告的面积最小.
解法2：设广告的高为宽分别为x cm，y cm，则每栏的高和宽分别为x－20，
其中x＞20，y＞25
两栏面积之和为2(x－20)
,由此得y=
广告的面积S=xy=x(
)＝x,
整理得S=
因为x－20＞0，所以S≥2
当且仅当
时等号成立，
此时有(x－20)2＝14400(x＞20)，解得x=140，代入y=
+25,得y＝175，
即当x=140，y＝175时，S取得最小值24500，
故当广告的高为140 cm，宽为175 cm时，可使广告的面积最小.
16. 证明：因为
为正实数，由平均不等式可得
即
所以
，
而
所以 
17. 解：（Ⅰ）
图像如下：
（Ⅱ）不等式
，即
，
由
得
．
由函数图像可知，原不等式的解集为
18.解：函数的定义域为
，且
19. （1）A
=
（2）
．
∴
20．解：对任意
,
,
,
,所以
,对任意的
，
，
，所以
0<
,令=
，
，
,所以
．
反证法:设存在两个
使得
,
则
由
，得
，所以
，矛盾，故结论成立。
，所以
+…
．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com