
题目列表(包括答案和解析)

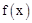 的极值;
的极值;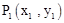 ,
,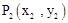 ,如果存在曲线上的点
,如果存在曲线上的点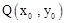 ,且
,且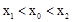 ,使得曲线在点
,使得曲线在点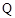 处的切线
处的切线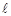 ∥
∥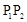 ,则称
,则称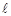 为弦
为弦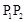 的伴随切线。特别地,当
的伴随切线。特别地,当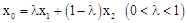 时,又称
时,又称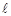 为
为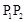 的λ-伴随切线。
的λ-伴随切线。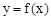 的任意一条弦均有伴随切线,并且伴随切线是唯一的;
的任意一条弦均有伴随切线,并且伴随切线是唯一的;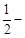 伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。设函数![]() ,
,
(Ⅰ)求函数![]() 的极大值;
的极大值;
(II)记![]() 的导函数为
的导函数为![]() ,若
,若![]() 时,恒有
时,恒有![]() 成立,试确定实数a的取值范围。
成立,试确定实数a的取值范围。
 。
。函数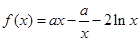
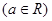
(Ⅰ)当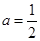 时,求f(x)的单调区间;
时,求f(x)的单调区间;
(Ⅱ)若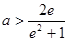 ,若
,若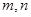 分别为
分别为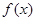 的极大值和极小值,若
的极大值和极小值,若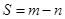 ,求
,求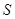 取值范围。
取值范围。
设函数![]() 的图象过点(-1,2)。
的图象过点(-1,2)。
(Ⅰ)试用a表示b;
(Ⅱ)当a=3时,求f(x)的单调区间与极值;
(Ⅲ)若a<0且f(-1)是函数f(x)的极小值,求a的取值范围。
一、选择题
1―5BABAB 6―10DBABA 11―12CC
|