用数学归纳法证明1＋2＋2²＋…＋2^n－1＝2ⁿ－1(n∈N^*)的过程中，第二步假设当n＝k(k∈N^*)时等式成立，则当n＝k＋1时应得到(　　)

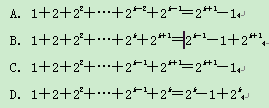
(1×2²-2×3²)+(3×4²-4×5²)+…+［(2n-1)(2n)²-2n(2n+1)²］=-n(n+1)(4n+3)(n∈N^*).

(1×2²-2×3²)+(3×4²-4×5²)+…+［(2n-1)(2n)²-2n(2n+1)²］=-n(n+1)(4n+3)(n∈N^*).

用数学归纳法证明" (1·22-2·32)+(3·42-4·52)+…+［(2n-1)·(2n)2-2n·(2n+1)2］＝-n(n+1)(4n+3),n∈N*"的第一步是: 当n＝1时,

 ∵左边＝_______, 右边＝______ (填计算结果)

∴左边＝右边, 等式成立.