
题目列表(包括答案和解析)
|
|
在平面直角坐标系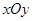 中,已知曲线
中,已知曲线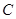 上任意一点到点
上任意一点到点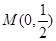 的距离与到直线
的距离与到直线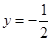 的距离相等.
的距离相等.
(Ⅰ)求曲线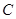 的方程;
的方程;
(Ⅱ)设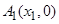 ,
,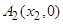 是
是 轴上的两点
轴上的两点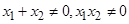 ,过点
,过点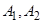 分别作
分别作 轴的垂线,与曲线
轴的垂线,与曲线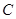 分别交于点
分别交于点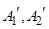 ,直线
,直线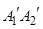 与x轴交于点
与x轴交于点 ,这样就称
,这样就称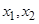 确定了
确定了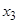 .同样,可由
.同样,可由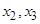 确定了
确定了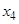 .现已知
.现已知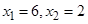 ,求
,求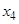 的值.
的值.
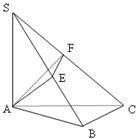
如图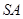 ⊥平面
⊥平面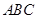 ,
,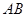 ⊥
⊥ ,过
,过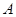 做
做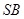
的垂线,垂足为 ,过
,过 做
做 的垂线,垂足为
的垂线,垂足为
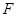 ,求证
,求证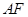 ⊥
⊥ 。以下是证明过程:
。以下是证明过程:
要证
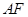 ⊥
⊥
只需证  ⊥平面
⊥平面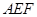
只需证 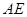 ⊥
⊥ (因为
(因为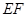 ⊥
⊥ )
)
只需证 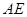 ⊥平面
⊥平面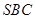
只需证 ① (因为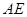 ⊥
⊥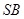 )
)
只需证  ⊥平面
⊥平面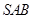
只需证 ② (因为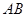 ⊥
⊥ )
)
由只需证 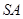 ⊥平面
⊥平面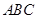 可知上式成立
可知上式成立
所以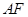 ⊥
⊥
把证明过程补充完整① ②
已知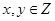 ,
,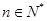 ,设
,设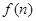 是不等式组
是不等式组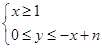 ,表示的平面区域内可行解的个数,由此可推出
,表示的平面区域内可行解的个数,由此可推出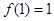 ,
,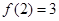 ,……, 则
,……, 则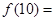 ( )
( )
A.45 B.55 C.60 D.100
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com