
题目列表(包括答案和解析)
| 分组 | 频数 | 频率 |
| [70,80) | 4 | 0.04 |
| [80,80) | 6 | 0.06 |
| [90,100) | 20 | 0.20 |
| [100,110) | 22 | 0.22 |
| [110,120) | 18 | b |
| [120,130) | a | 0.15 |
| [130,140) | 10 | 0.10 |
| [140,150) | 5 | 0.05 |
| 合计 | c | 1 |
在四棱锥 中,
中, 平面
平面 ,底面
,底面 为矩形,
为矩形, .
.
(Ⅰ)当 时,求证:
时,求证: ;
;
(Ⅱ)若 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.

【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时,底面ABCD为正方形,

又因为 ,
, ………………2分
………………2分
又 ,得证。
,得证。
第二问,建立空间直角坐标系,则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分
设BQ=m,则Q(1,m,0)(0《m《a》
要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得
由此知道a=2, 设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
解:(Ⅰ)当 时,底面ABCD为正方形,
时,底面ABCD为正方形,

又因为 ,
, 又
又
 ………………3分
………………3分
(Ⅱ) 因为AB,AD,AP两两垂直,分别以它们所在直线为X轴、Y轴、Z轴建立坐标系,如图所示,

则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分
设BQ=m,则Q(1,m,0)(0《m《a》要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得 由此知道a=2,
由此知道a=2,
设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
| 平面几何选讲 | 极坐标与参数方程 | 不等式选讲 | 合计 | |
| 男同学(人数) | 12 | 4 | 6 | 22 |
| 女同学(人数) | 0 | 8 | 12 | 20 |
| 合计 | 12 | 12 | 18 | 42 |
| 几何类 | 代数类 | 合计 | |
| 男同学(人数) | 16 | 6 | 22 |
| 女同学(人数) | 8 | 12 | 20 |
| 合计 | 24 | 18 | 42 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 平面几何选讲 | 极坐标与参数方程 | 不等式选讲 | 合计 | |
| 男同学(人数) | 12 | 4 | 6 | 22 |
| 女同学(人数) | 0 | 8 | 12 | 20 |
| 合计 | 12 | 12 | 18 | 42 |
| 几何类 | 代数类 | 合计 | |
| 男同学(人数) | 16 | 6 | 22 |
| 女同学(人数) | 8 | 12 | 20 |
| 合计 | 24 | 18 | 42 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(本小题满分12分)
某校共有800名学生,高三一次月考之后,为了了解学生学习情况,用分层抽样方法从中抽出若干学生此次数学成绩,按成绩分组,制成如下的频率分布表:
|
组号 |
第 一 组 |
第 二 组 |
第 三 组 |
第 四 组 |
第 五 组 |
第 六 组 |
第 七 组 |
第 八 组 |
合计 |
|
分组 |
|
|
|
|
|
|
|
|
|
|
频数 |
4 |
6 |
20 |
22 |
18 |
|
10 |
5 |
|
|
频率 |
0.04 |
0.06 |
0.20 |
0.22 |
|
0.15 |
0.10 |
0.05 |
1 |
(Ⅰ) 李明同学本次数学成绩为103分,求他被抽中的概率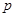 ;
;
(Ⅱ) 为了了解数学成绩在120分以上的学生的心理状态,现决定在第六、七、八组中用分层抽样方法抽取6名学生的成绩,并在这6名学生中在随机抽取2名由心理老师张老师负责面谈,求第七组至少有一名学生与张老师面谈的概率;
(Ⅲ) 估计该校本次考试的数学平均分。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com