
题目列表(包括答案和解析)
函数 与
与 互为反函数,且
互为反函数,且 ,若
,若 在[-1,1]上的最大值比最小值大2,则
在[-1,1]上的最大值比最小值大2,则 的值为
。
的值为
。
函数 与
与 互为反函数,且
互为反函数,且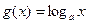 ,若
,若 在[-1,1]上的最大值比最小值大2,则
在[-1,1]上的最大值比最小值大2,则 的值为 。
的值为 。
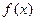 与
与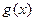 互为反函数,且
互为反函数,且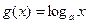 ,若
,若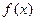 在[-1,1]上的最大值比最小值大2,则
在[-1,1]上的最大值比最小值大2,则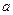 的值为 。
的值为 。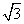 sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π。
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π。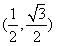 ,求f(θ)的值。
,求f(θ)的值。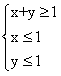 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值。
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值。
1.D 2.A 3.B 4.D 5.B 6.C 7.C 8.B 9.C 10.A
11.25,60,15 12.0.469 13..files/image092.gif) 14.
14..files/image094.gif)
15..files/image096.gif)
16.解:(1)由.files/image098.gif) …………3分
…………3分
.files/image100.gif)
.files/image102.gif) 是增函数…………7分
是增函数…………7分
(2)当.files/image104.gif)
.files/image106.gif) ………………12分
………………12分
17.解:(1).files/image108.gif) ,………………2分
,………………2分
.files/image110.gif) ,………………4分
,………………4分
切点为(1,―1),则.files/image112.gif) 的图象经过点(1,―1)
的图象经过点(1,―1)
得.files/image114.gif)
.files/image116.gif) ……………………7分
……………………7分
(2)由.files/image118.gif) ,
,
.files/image120.gif) (闭区间也对)………12分
(闭区间也对)………12分
18.解:(1).files/image122.gif)
.files/image124.gif) 不在集合A中。 ……………………3分
不在集合A中。 ……………………3分
又.files/image126.gif) , ………………5分
, ………………5分
.files/image128.gif)
.files/image130.gif) ……………………8分
……………………8分
(2)当.files/image132.gif) , ………………11分
, ………………11分
又由已知.files/image134.gif) ,
,
因此所求的实数k的取值范围是.files/image136.gif) ………………12分
………………12分
19.解:(1)参加单打的队员有.files/image138.gif) 种方法。
种方法。
参加双打的队员有.files/image140.gif) 种方法。
种方法。
所以,高三(1)班出场阵容共有.files/image142.gif) (种)。 ………………6分
(种)。 ………………6分
(2)高三(1)班代表队连胜两盘,可分为第一盘、第二盘胜或第一盘负,其余两盘胜,
所以,连胜两盘的概率为.files/image144.gif) ………………12分
………………12分
20.(1)依题意.files/image146.gif)
.files/image148.gif)
此函数的定义域为(7,40)。 ………………6分
(2).files/image150.gif) ………………8分
………………8分
当.files/image152.gif) (元),
(元),
当.files/image154.gif) (元)。 ………………12分
(元)。 ………………12分
综上可得当.files/image156.gif) 时,该特许专营店获得的利润最大为32400元。………………13分
时,该特许专营店获得的利润最大为32400元。………………13分
21.解:(1).files/image158.gif) 恒成立,
恒成立,
知.files/image160.gif)
从而.files/image162.gif) ………………4分
………………4分
(2)由(1)可知.files/image164.gif) ,
,
由于.files/image166.gif) 是单调函数,
是单调函数,
知.files/image168.gif) ………………8分
………………8分
(3).files/image170.gif)
.files/image172.gif) 上是增函数,
上是增函数,
.files/image174.gif)
.files/image176.gif)
………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com