
题目列表(包括答案和解析)
(12分)已知函数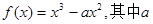 为正常数。
为正常数。
(1)设当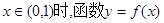 图象上任一点P处的切线的斜率为k,若
图象上任一点P处的切线的斜率为k,若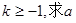 的取值范围;
的取值范围;
(2)当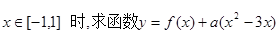 的最大值。
的最大值。
已知函数 为正常数。
为正常数。
(1)设当 图象上任一点P处的切线的斜率为k,若
图象上任一点P处的切线的斜率为k,若 的取值范围;
的取值范围;
(2)当 的最大值。
的最大值。
 .
. ,求实数a的取值范围;
,求实数a的取值范围; ;
; (m>0)有唯一解,求m的值.
(m>0)有唯一解,求m的值.已知函数f(x)=x3-ax2,其中a为正常数.
(1)设当x∈(0,1)时,函数y=f(x)图象上任一点P处的切线的斜率为k,若k≥-1,求a的取值范围;
(2)当x∈[-1,1]时,求函数y=f(x)+a(x2-3x)的最大值.
设函数![]()
(Ⅰ)当![]() 时,求f(x)的最大值;
时,求f(x)的最大值;
(Ⅱ)令![]() ,(0<x≤3),其图象上任意一点P(x0,y0)处切线的斜率k≤
,(0<x≤3),其图象上任意一点P(x0,y0)处切线的斜率k≤![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(Ⅲ)当a=0,b=-1,方程2 mf(x)=x2有唯一实数解,求正数m的值.
一、选择题(本大题共12小题,每小题5分,共60分。
1―5 BBACB 6―10 ADCDD 11―12 AB
二、填空题(本大题共4小题,每小题6分,共16分,
13.14 14.2 15.30 16.①③
三、解答题(本大题共6小题,共计76分)
17.解:(1) …………2分
…………2分

(2)由题设, …………10分
…………10分
 …………12分
…………12分
18.解:(1)记“第一次与第二次取到的球上的号码的和是
 …………5分
…………5分
所以第一次与第二次取到的地球上的号码的和是4的概率 …………6分
…………6分
(2)记“第一次与第二次取到的上的号码的积不小于
 …………11分
…………11分
|