查看答案和解析>>

有一幅椭圆型彗星轨道图，长4 cm，高，如下图，已知O为椭圆中心，A₁，A₂是长轴两端点，太阳位于椭圆的左焦点F处．

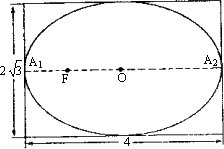
(Ⅰ)建立适当的坐标系，写出椭圆方程，并求出当彗星运行到太阳正上方时二者在图上的距离；

(Ⅱ)直线l垂直于A₁A₂的延长线于D点，|OD|＝4，设P是l上异于D点的任意一点，直线A₁P，A₂P分别交椭圆于M、N(不同于A₁，A₂)两点，问点A₂能否在以MN为直径的圆上？试说明理由．

查看答案和解析>>

一、选择题（本大题共10小题，每题5分，共50分）

1．C         2．A        3．B        4．D           5．B

6．B         7．C        8．D        9．D          10．A

二、填空题（本大题共7小题，每题4分，共28分）

11．2        12．45        13．       14．

15．1        16．144       17．

三、解答题（本大题共5小题，第18―20题各14分，第21、22题各15分，共72分）

18．（1）因为（4分）

        所以

   （Ⅱ）由（I）得，

                         （10分）

         因为所以，所以（12分）

         因此，函数的值域为。（14分）

19．（I）因为，所以平面。 （3分）

又因为平面所以    ①（5分）

在中，，由余弦定理，

得

因为，所以，即。②  （7分）

由①，②及，可得平面   （8分）

（Ⅱ）方法一；

在中，过作于，则，所以平面

在中，过作于，连，则平面，

所以为二面角的平面角   （11分）

在中，求得，

在中，求得，

所以所以。

因此，所求二面角的大小的余弦值为。

方法二：

如图建立空间直角坐标系 （9分）

则

设平面的法向量为，

则

所以，取，

则  （11分）

又设平面的法向量为，

则

，取，则（13分）

所以，

因此，所求二面角的大小余弦值为。

20．（I）（6分）

   （Ⅱ）

1

2

3

4

5

       （14分）

21．（I）由题意得    （3分）

     解得（5分）

     所以椭圆方程为   （6分）

（Ⅱ）直线方程为，则的坐标为  （7分）

设则，

直线方程为令，得的横坐标为

①    （10分）

又得得， （12分）

代入①得， （14分）

得，       为常数4   （15分）

22．（I）   （2分）

     由于，故尝时，，所以，   （4分）

     故函数在上单调递增。   （5分）

   （Ⅱ）令，得到   （6分）

     的变化情况表如下：   （8分）

0

一

0

+

极小值

      因为函数 有三个零点，所以有三个根，

      有因为当时，，

      所以，故   （10分）

   （Ⅲ）由（Ⅱ）可知在区间上单调递减，在区间上单调递增。

     所以    （11分）

     记则（仅在时取到等号），

     所以递增，故，

     所以    （13分）

     于是

     故对

     ，所以   （15分）