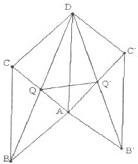如图，矩形ABCD与矩形AB′C′D全等，且所在平面所成的二面角为a，记两个矩形对角线的交点分别为Q，Q′，AB=a，AD=b．
（1）求证：QQ′∥平面ABB′；
（2）当b=

2

a，且a=

π

3

时，求异面直线AC与DB′所成的角；
（3）当a＞b，且AC⊥DB'时，求二面角a的余弦值（用a，b表示）．

查看答案和解析>>

查看答案和解析>>

某先生居住在城镇的A处，准备开车到单位B处上班，若该地各路段发生堵车事件都是独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率，如图．（ 例如：A→C→D算作两个路段：路段AC发生堵车事件的概率为

1

10

，路段CD发生堵车事件的概率为

1

15

）．
（1）请你为其选择一条由A到B的路线，使得途中发生堵车事件的概率最小；
（2）若记ξ路线A→（3）C→（4）F→（5）B中遇到堵车次数为随机变量ξ，求ξ的数学期望Eξ．

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

一、选择题(每小题5分，共50分)

  1．C  2．B  3．D  4．A  5．C  6．B  7．A  8．C  9．B  10．D

二、填空题(每小题4分．共24分)

  11．5  12．4   13．3825   14． 15．   16．3

三．解答题(本大题共6小题，共76分)

17．(本题12分)

解：(Ⅰ)∵，

∴          ………………………(2分)

∴    ………………………(3分)

∴              ……………………(4分)

∵在中，

∴                             ………………………(5分)

(Ⅱ)设分别是中的对边，

∵?

∴

∴    ①                                          ……………………(6分)

由正弦定理：，得              ……………………(7分)

∴

∴    ②                                          ……………………(8分)

由①②解得                                    ……………………(9分)

由余弦定理，得                       ………………(10分)

                                                        ………………(11分)

∴，即边的长为。                              ……………………(12分)

18．(本题12分]

解：(Ⅰ)∵是偶函数，

∴，即            ……(2分)

                                  ………………………………(4分)

∴对一切恒成立。

∴                                    ……………………………………(6分)

(Ⅱ)由                            ………………(7分)

                                           …………………(8分)

∵错误！不能通过编辑域代码创建对象。≥                                           ……………………(10分)

∴≥                                    …………………(11分)

∴≤

∴若使方程有解，则的取值范围是≤          ………………(12分)

19．(本题12分)

解：(Ⅰ) ∵分别是的中点，

∴且                                  ……………………(1分)

∵平面,平面

∴平面                                   …………………………(2分)

∵平面平面，平面

∴                                          …………………………(4分)

∵是的中点，

∴是的中点．

∴                               ………………………(5分)

∴

∴四边形是平行四边形                         …………………………(6 分)

(Ⅱ)当时，平面平面                   …………………(8分)

在上取一点，连接

当时，

∵，

∴

即当时，，                    ……………………(9分)

∵，，

∴平面                                       ……………………(10分)

∵

∴平面                                 ……………………………(11分)

∵平面

∴平面平面                     …………………………………(12分)

20．(本题12分)

解：(Ⅰ) ∵

∴                           ………………………………(2分)

∵在区间上为减函数

∴≤O在区间上恒成立                      …………………………(3分)

∵是开口向上的抛物线

        ≤      ≤

∴只需              即                               …………………………(5分)

        ≤       ≤

∴≤≤                             ………………………………………(6分)

(Ⅱ)当时，                     

∴存在，使得

∴在区间内有且只有一个极小值点                      ……………(8分)

当时                      

∴存在，使得

∴在区间内有且只有一个极大值点                     ……………(10分)

当≤≤时，由(Ⅰ)可知在区间上为减函数

∴在区间内没有极值点．

综上可知，当时，在区间内的极值点个数为

当≤≤时，在区间内的极值点个数为          ………(12分)

21．(本题14分)

解：(Ⅰ)设椭圆的长半轴长为，短半轴长，半焦距为，

由离心率，得

∵

∴            ①                                     …………………(2分)

∵直线的方程为，原点到直线的距离为，

∴  ②                                     …………………(4分)

①代人②，解得                            ………………………(6分)

∴椭圆的标准方程为                        …………………………(7分)

(Ⅱ) ∵

∴?=

∴?=?(-)=²                                    …………………(9分)

设,则，即                     ………………(10分)

∴?=²