题目列表(包括答案和解析)
已知函数
，
.
（Ⅰ）若函数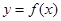
依次在
处取到极值.求
的取值范围；
（Ⅱ）若存在实数
，使对任意的
，不等式
恒成立.求正整数
的最大值.
【解析】第一问中利用导数在在处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
第二问中，利用存在实数，使对任意的，不等式
恒成立转化为
，恒成立，分离参数法求解得到范围。
解：（1）
①
（2）不等式 ，即
，即
.
转化为存在实数
，使对任意的
，不等式恒成立.
即不等式
在上恒成立.
即不等式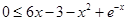
在上恒成立.
设
，则.
设
，则
，因为，有
.
故
在区间上是减函数。又
故存在
，使得
.
当
时，有
，当
时，有
.
从而
在区间
上递增，在区间
上递减.
又
[来源:]
所以当
时，恒有
；当
时，恒有
；
故使命题成立的正整数m的最大值为5
已知函数
，
．
（Ⅰ）若函数
和函数
在区间
上均为增函数，求实数
的取值范围；
（Ⅱ）若方程
有唯一解，求实数
的值．
【解析】第一问， 
当0<x<2时，
，当x>2时，
，
要使
在(a,a+1)上递增，必须
如使
在(a,a+1)上递增，必须
，即
由上得出，当
时，在
上均为增函数
（Ⅱ）中方程有唯一解
有唯一解
设
（x>0）
随x变化如下表
|
x |
|
|
|
|
|
- |
|
+ |
|
|
|
极小值 |
|
由于在
上，
只有一个极小值，
的最小值为-24-16ln2，
当m=-24-16ln2时，方程有唯一解得到结论。
（Ⅰ）解：
当0<x<2时，，当x>2时，，
要使在(a,a+1)上递增，必须
如使在(a,a+1)上递增，必须，即
由上得出，当时，在上均为增函数 ……………6分
（Ⅱ）方程有唯一解有唯一解
设
（x>0）
随x变化如下表
|
x |
|
|
|
|
|
- |
|
+ |
|
|
|
极小值 |
|
由于在上，只有一个极小值，的最小值为-24-16ln2，
当m=-24-16ln2时，方程有唯一解
（本题满分12分）已知函数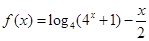
．
(1)判断f(x)的奇偶性，并说明理由；
(2)若方程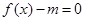
有解，求m的取值范围；
【解析】第一问利用函数的奇偶性的定义可以判定定义域和f(x)与f(-x)的关系从而得到结论。
第二问中，利用方程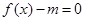有解，说明了参数m落在函数y=f(x)的值域里面即可。
（本题16分）已知函数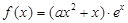
，其中e是自然数的底数，
，
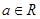（1）当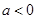
时，解不等式
；
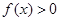（2）若当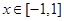
时，不等式
恒成立，求a的取值范围；
（3）当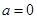
时，试判断：是否存在整数k，使得方程
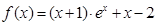在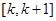
上有解？若存在，请写出所有可能的k的值；若不存在，说明理由。
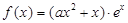，其中e是自然数的底数，
，
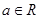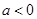时，解不等式
；
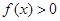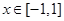时，不等式
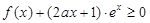恒成立，求a的取值范围；
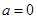时，试判断：是否存在整数k，使得方程
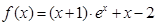在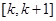
一、选择题(每小题5分，共50分)
1．C 2．B 3．D 4．A 5．C 6．B 7．A 8．C 9．B 10．D
二、填空题(每小题4分．共24分)
11．5
12．4 13．3825 14．
15．
16．3
三．解答题(本大题共6小题，共76分)
17．(本题12分)
解：(Ⅰ)∵
，
∴
………………………(2分)
∴
………………………(3分)
∴
……………………(4分)
∵在
中，
∴
………………………(5分)
(Ⅱ)设
分别是中
的对边，
∵?
∴
∴
① ……………………(6分)
由正弦定理：
，得 
……………………(7分)
∴
∴
② ……………………(8分)
由①②解得
……………………(9分)
由余弦定理，得
………………(10分)
………………(11分)
∴
，即边
的长为
。
……………………(12分)
18．(本题12分]
解：(Ⅰ)∵
是偶函数，
∴
，即
……(2分)
………………………………(4分)
∴
对一切
恒成立。
∴
……………………………………(6分)
(Ⅱ)由
………………(7分)
…………………(8分)
∵错误！不能通过编辑域代码创建对象。≥
……………………(10分)
∴
≥
…………………(11分)
∴
≤
∴若使方程
有解，则的取值范围是≤
………………(12分)
19．(本题12分)
解：(Ⅰ) ∵
分别是
的中点，
∴
且
……………………(1分)
∵
平面
,
平面
∴
平面
…………………………(2分)
∵
平面
平面
，
平面
∴
…………………………(4分)
∵
是
的中点，
∴
是
的中点．
∴
………………………(5分)
∴
∴四边形是平行四边形 …………………………(6 分)
(Ⅱ)当
时，平面
平面
…………………(8分)
在
上取一点，
连接
当
时，
∵
，
∴
即当时，
，
……………………(9分)
∵，，
∴
平面
……………………(10分)
∵
∴
平面
……………………………(11分)
∵平面
∴平面
平面
…………………………………(12分)
20．(本题12分)
解：(Ⅰ) ∵
∴
………………………………(2分)
∵在区间
上为减函数
∴
≤O在区间上恒成立 …………………………(3分)
∵是开口向上的抛物线
≤
≤
∴只需 即 …………………………(5分)
≤ 
≤
∴
≤
≤
………………………………………(6分)
(Ⅱ)当
时，
∴存在
，使得
∴在区间内有且只有一个极小值点 ……………(8分)
当
时
∴存在，使得
∴在区间内有且只有一个极大值点 ……………(10分)
当≤≤时，由(Ⅰ)可知在区间上为减函数
∴在区间内没有极值点．
综上可知，当时，
在区间内的极值点个数为
当≤≤时，在区间内的极值点个数为
………(12分)
21．(本题14分)
解：(Ⅰ)设椭圆的长半轴长为，短半轴长
，半焦距为
，
由离心率
，得
∵
∴
① …………………(2分)
∵直线的方程为
，原点
到直线的距离为
，
∴
② …………………(4分)
①代人②，解得
………………………(6分)
∴椭圆的标准方程为
…………………………(7分)
(Ⅱ) ∵
∴?=
∴?=?(-)=2 …………………(9分)
设
,则，即
………………(10分)
∴?=2
同步练习册答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
