在四棱锥中，平面，底面为矩形，.

（Ⅰ）当时，求证：；

（Ⅱ）若边上有且只有一个点，使得，求此时二面角的余弦值.

【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时，底面ABCD为正方形，

又因为,………………2分

又，得证。

第二问，建立空间直角坐标系，则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分

设BQ=m，则Q(1，m,0)(0《m《a》

要使，只要

所以，即………6分

由此可知时，存在点Q使得

当且仅当m=a-m，即m=a/2时，BC边上有且只有一个点Q，使得

由此知道a=2,  设平面POQ的法向量为

,所以    平面PAD的法向量

则的大小与二面角A-PD-Q的大小相等所以

因此二面角A-PD-Q的余弦值为

解：(Ⅰ)当时，底面ABCD为正方形，

又因为,又………………3分

(Ⅱ) 因为AB,AD,AP两两垂直，分别以它们所在直线为X轴、Y轴、Z轴建立坐标系，如图所示，

则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分

设BQ=m，则Q(1，m,0)(0《m《a》要使，只要

所以，即………6分

由此可知时，存在点Q使得

当且仅当m=a-m，即m=a/2时，BC边上有且只有一个点Q，使得由此知道a=2,

设平面POQ的法向量为

,所以    平面PAD的法向量

则的大小与二面角A-PD-Q的大小相等所以

因此二面角A-PD-Q的余弦值为

 

已知m>1，直线，椭圆C：，、分别为椭圆C的左、右焦点.

（Ⅰ）当直线过右焦点时，求直线的方程;

（Ⅱ）设直线与椭圆C交于A、B两点，△A、△B的重心分别为G、H.若原点O在以线段GH为直径的圆内，求实数m的取值范围.[

【解析】第一问中因为直线经过点（，0），所以＝，得.又因为m>1，所以，故直线的方程为

第二问中设，由，消去x，得，

则由，知<8,且有

由题意知O为的中点.由可知从而，设M是GH的中点，则M（）.

由题意可知，2|MO|<|GH|,得到范围

 

 [番茄花园1] 为了能更好地了解鲸的生活习性，某动物研究所在受伤的鲸身上安装了电子监测装置，从海岸放归点A处（如图所示）把它放归大海，并沿海岸线由西到东不停地对鲸进行了40分钟的跟踪观测，每隔10分钟踩点测得数据如下表（设鲸沿海面游动）。然后又在观测站B处对鲸进行生活习性的详细观测。已知AB=15km，观测站B的观测半径为5km.

观测时刻t (分钟)	跟踪观测点到放归点距离a(km)	鲸位于跟踪观测点正北方向的距离b(km)
10	1	1
20	2
30	3
40	4	2

   （I）根据表中数据：（1）计算鲸沿海岸线方向运动的速度，（2）写出a、b满足的关系式，并画出鲸的运动路线简图；

   （II）若鲸继续以（I）－（2）中的运行路线运动，则鲸经过多少分钟（从放归时计时），可进入前方观测站B的观测范围。()

 

 

 

 

 

 

 

 

---

 [番茄花园1]18．

设f (x)＝sin 2x＋(sin x－cos x)(sin x＋cos x)，其中x∈R．

(Ⅰ) 该函数的图象可由 的图象经过怎样的平移和伸缩变换得到？

(Ⅱ)若f (θ)＝，其中，求cos(θ＋)的值；

【解析】第一问中，

即变换分为三步，①把函数的图象向右平移，得到函数的图象；

②令所得的图象上各点的纵坐标不变，把横坐标缩短到原来的倍，得到函数的图象；

③令所得的图象上各点的横坐标不变，把纵坐标伸长到原来的2倍，得到函数的图象；

第二问中因为，所以，则，又 ，,从而

进而得到结论。

(Ⅰ) 解：

即。…………………………………3分

变换的步骤是：

①把函数的图象向右平移，得到函数的图象；

②令所得的图象上各点的纵坐标不变，把横坐标缩短到原来的倍，得到函数的图象；

③令所得的图象上各点的横坐标不变，把纵坐标伸长到原来的2倍，得到函数的图象；…………………………………3分

(Ⅱ) 解：因为，所以，则，又 ，,从而……2分

(1)当时，；…………2分

(2)当时；

 

设椭圆（常数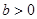）的左右焦点分别为，是直线上的两个动点，．

（1）若，求的值；

（2）求的最小值．

【解析】第一问中解：设，则

由得    由，得

  ② 

第二问易求椭圆的标准方程为：

，

所以，当且仅当或时，取最小值．

解：设， ……………………1分

则，由得     ①……2分

（1）由，得  ②   ……………1分

    ③    ………………………1分

由①、②、③三式，消去，并求得． ………………………3分

（2）解法一：易求椭圆的标准方程为：．………………2分

， ……4分

所以，当且仅当或时，取最小值．…2分

解法二：， ………………4分

所以，当且仅当或时，取最小值