
题目列表(包括答案和解析)
 (2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0).
(2011•盐城二模)如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成.两相接点M,N均在直线x=5上,圆弧C1的圆心是坐标原点O,半径为r1=13; 圆弧C2过点A(29,0).| 30 |
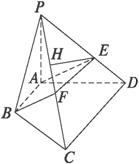
(1)点F在线段PC上运动,且设![]() =λ,问当λ为何值时,BF∥平面PAD?并证明你的结论;
=λ,问当λ为何值时,BF∥平面PAD?并证明你的结论;
(2)二面角F—CD—B为45°,求二面角B—PC—D的大小;
(3)在(2)的条件下,若AD=2,CD=3,求点A到平面PBC的距离.
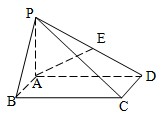 (2008•闸北区二模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,BC=2.
(2008•闸北区二模)如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=1,BC=2.| 2 |

(1)点F在线段PC上运动,且设![]() ,问当λ为何值时,BF∥平面PAD?并证明你的结论;
,问当λ为何值时,BF∥平面PAD?并证明你的结论;
(2)若二面角F-CD-B为![]() ,求二面角B-PC-D的大小;
,求二面角B-PC-D的大小;
(3)在(2)的条件下,若AD=2,CD=3,求点A到平面PBC的距离.
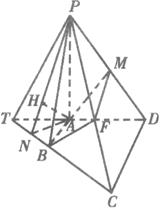
(1)点F在线段PC上运动,且设![]() =λ,问当λ为何值时,BF∥平面PAD?并证明你的结论;
=λ,问当λ为何值时,BF∥平面PAD?并证明你的结论;
(2)若二面角F-CD-B为45°,求二面角B-PC-D的大小;
(3)在(2)的条件下,若AD=2,CD=3,求点A到平面PBC的距离.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com