如图，在三棱柱中，侧面，为棱上异于的一点，，已知，求：

（Ⅰ）异面直线与的距离；

（Ⅱ）二面角的平面角的正切值.

【解析】第一问中，利用建立空间直角坐标系

解：（I）以B为原点，、分别为Y,Z轴建立空间直角坐标系.由于，

在三棱柱中有

,

设

又侧面，故. 因此是异面直线的公垂线，则，故异面直线的距离为1.

（II）由已知有故二面角的平面角的大小为向量与的夹角.

如图6，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是等腰梯形，AD∥BC，AC⊥BD.

（Ⅰ）证明：BD⊥PC；

（Ⅱ）若AD=4，BC=2，直线PD与平面PAC所成的角为30°，求四棱锥P-ABCD的体积.

【解析】（Ⅰ）因为

又是平面PAC内的两条相较直线，所以BD平面PAC，

而平面PAC，所以.

（Ⅱ）设AC和BD相交于点O，连接PO，由（Ⅰ）知，BD平面PAC，

所以是直线PD和平面PAC所成的角，从而.

由BD平面PAC，平面PAC，知.在中，由，得PD=2OD.因为四边形ABCD为等腰梯形，，所以均为等腰直角三角形，从而梯形ABCD的高为于是梯形ABCD面积

在等腰三角形ＡＯＤ中，

所以

故四棱锥的体积为.

【点评】本题考查空间直线垂直关系的证明，考查空间角的应用，及几何体体积计算.第一问只要证明BD平面PAC即可，第二问由（Ⅰ）知，BD平面PAC，所以是直线PD和平面PAC所成的角，然后算出梯形的面积和棱锥的高，由算得体积

已知函数，.

（Ⅰ）若函数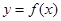依次在处取到极值.求的取值范围；

（Ⅱ）若存在实数，使对任意的，不等式 恒成立.求正整数的最大值.

【解析】第一问中利用导数在在处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。

第二问中，利用存在实数，使对任意的，不等式 恒成立转化为，恒成立，分离参数法求解得到范围。

解：（1）

①

（2）不等式 ，即，即.

转化为存在实数，使对任意的，不等式恒成立.

即不等式在上恒成立.

即不等式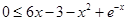在上恒成立.

设，则.

设，则，因为，有.

故在区间上是减函数。又

故存在，使得.

当时，有，当时，有.

从而在区间上递增，在区间上递减.

又[来源:]

所以当时，恒有；当时，恒有；

故使命题成立的正整数m的最大值为5

汽车行驶中，由于惯性作用，刹车后还要继续向前滑行一段距离才能停住，我们称这段距离为“刹车距离”．刹车距离是分析事故的重要因素．在一个限速40千米/时以内的弯道上，甲、乙两辆汽车相向而行，当司机发现有情况时，同时刹车，但汽车还是相撞了．事故发生后，现场测得甲车的刹车距离超过12米，但不超过15米；乙车刹车距离超过10米，但不超过12米．又知甲、乙车型的刹车距离s(米)与车速x(千米/时)之间分别有下列关系：

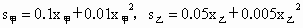则因超速行驶而应负主要责任的是__________．