
题目列表(包括答案和解析)
心理学家研究发现:一般情况下,学生的注意力随着老师讲课时间的变化而变化.讲课开始时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力y随时间t的变化规律有如下关系式:
y=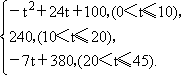
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较,何时学生的注意力更集中?
(2)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(3)一道数学综合题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?如果不能讲解完,说明理由;如果能够讲解完,请说明老师应该在哪个时间段内讲解.
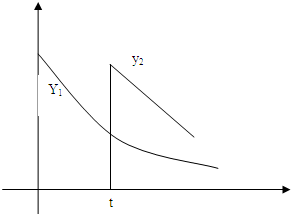 心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量为1,则x天后的存留量y1=
心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量为1,则x天后的存留量y1=| 4 |
| x+4 |
| a |
| (t+4)2 |
心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量记为1,则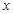 天后的存留量
天后的存留量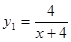 ;若在
;若在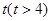 天时进行第一次复习,则此时知识存留量比未复习情况下增加一倍(复习时间忽略不计),其后存储量
天时进行第一次复习,则此时知识存留量比未复习情况下增加一倍(复习时间忽略不计),其后存储量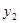 随时间变化的曲线恰为直线的一部分,其斜率为
随时间变化的曲线恰为直线的一部分,其斜率为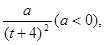 存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时此刻为“二次复习最佳时机点”.
存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时此刻为“二次复习最佳时机点”.
(1)若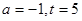 ,求“二次最佳时机点”;
,求“二次最佳时机点”;
(2)若出现了“二次复习最佳时机点”,求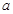 的取值范围.
的取值范围.
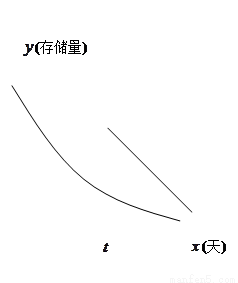
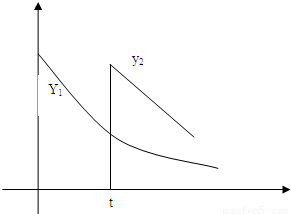 心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量为1,则x 天后的存留量
心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量为1,则x 天后的存留量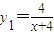 ;若在t(t>0)天时进行第一次复习,则此时这似乎存留量比未复习情况下增加一倍(复习的时间忽略不计),其后存留量y2随时间变化的曲线恰好为直线的一部分,其斜率为
;若在t(t>0)天时进行第一次复习,则此时这似乎存留量比未复习情况下增加一倍(复习的时间忽略不计),其后存留量y2随时间变化的曲线恰好为直线的一部分,其斜率为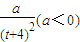 ,存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时刻为“二次复习最佳时机点”
,存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时刻为“二次复习最佳时机点” 天后
天后 的存留量
的存留量 ;若在
;若在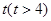 天时进行第一次复习,则此时知识存留量比未复习情况下增加一倍(复习时间忽略不计),其后存储量
天时进行第一次复习,则此时知识存留量比未复习情况下增加一倍(复习时间忽略不计),其后存储量 随时间变化的曲线恰为直线的一部分,其斜率为
随时间变化的曲线恰为直线的一部分,其斜率为 存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时此刻为“二次复习最佳时机点”.
存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时此刻为“二次复习最佳时机点”. ,求“二次最佳时机点”;
,求“二次最佳时机点”; 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com