练习册

  • 练习册
  • 试题
    我们已经学习用概率表示一个事件在一次试验或观测中发生的可能性的大小.它是在-之间的一个数.将这个事件记为.用表示事件发生的概率.用它来刻画此随机事件发生可能性的大小.那么又怎样确定一事件发生的概率呢? 在一章中.我们曾设计了一个抛掷硬币的模拟试验.图3-1-1是连续8次模拟试验的结果: AB1模拟次数10 【查看更多】

     

    题目列表(包括答案和解析)

    我们已经学过了等差数列,你是否想到过有没有等和数列呢?

    (1)类比“等差数列”给出“等和数列”的定义.

    (2)探索等和数列{an}的奇数项与偶数项各有什么特点,并加以说明.

    (3)在等和数列{an}中,如果a1=a,a2=b,求它的前n项和Sn.?

    查看答案和解析>>

    我们已经学过了等差数列,你是否想到过有没有等和数列呢?

    (1)类比“等差数列”给出“等和数列”的定义.

    (2)探索等和数列{an}的奇数项与偶数项各有什么特点,并加以说明.

    (3)在等和数列{an}中,如果a1=a,a2=b,求它的前n项和Sn.?

    查看答案和解析>>

    在直角三角形中，我们已经学过三边之间的一个重要关系式，如图1-4-3，在Rt△ABC中，∠C＝90°，那么AC2＋BC2=AB2，这一结论被称作勾股定理，同样是在直角三角形中，勾股定理和射影定理有什么联系？如何说明这种联系？

    图1-4-3

    查看答案和解析>>

    （2013•梅州二模）有甲乙两个班进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩后，得到如下列联表．
    优秀 非优秀 总计
    甲班 10
    乙班 30
    合计 105
    已知在全部105人中随机抽取1人为优秀的概率为
    2
    7
    ．
    （1）请完成上面的联表；
    （2）根据列联表的数据，若按95%的可靠性要求，能否认为“成绩与班级有关系”；
    （3）若按下面的方法从甲班优秀的学生抽取一人：把甲班10优秀的学生按2到11进行编号，先后两次抛掷一枚骰子，出现的点数之和为被抽取的序号．试求抽到6号或10号的概率．
    参考公式：K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，其中n=a+b+c+d．
    概率表
    P（K2≥k0） 0.15 0.10 0.05 0.025 0.010
    k0 2.072 2.706 3.841 5.024 6.635

    查看答案和解析>>

    为了判断高中学生选读文科是否与性别有关，现随机抽取50名学生，得到如下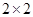列联表：

     

    理科

       文科 

        合计

           男

         13

        10

         23

           女

         7

        20

         27

          合计

         20

        30

         50

    已知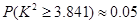,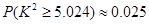，根据表中数据，得到

    ，则在犯错误的概率不超过           的前提下可以认为选读文科与性别是有关系的。

     

    查看答案和解析>>


    同步练习册答案