题目列表(包括答案和解析)
（本小题共14分）
已知函数
（1）试用含有a的式子表示b，并求
的单调区间；
（2）设函数的最大值为
，试证明不等式：
（3）首先阅读材料：对于函数图像上的任意两点
，如果在函数图象上存在点
，使得在点M处的切线
，则称AB存在“相依切线”特别地，当
时，则称AB存在“中值相依切线”。
请问在函数的图象上是否存在两点，使得AB存在“中值相依切线”？若存在，求出一组A、B的坐标；若不存在，说明理由。
（本小题共14分）
已知函数
在
时取得极值，曲线
在
处的切线的斜率为
；函数
，
，函数
的导函数
的最小值为
．
（Ⅰ）求函数
的解析式；
（Ⅱ）求实数
的值；
(Ⅲ) 求证：
．
（本小题共14分）
已知椭圆
的焦点是
,
,点
在椭圆上且满足
.
（Ⅰ）求椭圆的标准方程；
（Ⅱ）设直线
与椭圆的交点为
，
.
(i)求使
的面积为
的点的个数；
(ii)设
为椭圆上任一点，
为坐标原点，
，求
的值.
. （本小题共14分）
已知函数
，其中
.
(Ⅰ)若b>2a,且
的最大值为2,最小值为-4,试求函数f(x)的最小值；
(Ⅱ)若对任意实数x，不等式
恒成立，且存在
使得
成立，求c的值.
(本小题共14分)已知
是由满足下述条件的函数构成的集合：对任意
，①方程
有实数根；②函数
的导数
满足
．
（Ⅰ）判断函数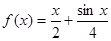
是否是集合中的元素，并说明理由；
（Ⅱ）集合中的元素具有下面的性质：若的定义域为
，则对于任意
，都存在
，使得等式
成立．试用这一性质证明：方程有且只有一个实数根；
（Ⅲ）对任意，且
，求证：对于定义域中任意的
，
，
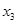，当
，且
时，
.
一、选择题（本大题共8小题，每小题5分，共40分）
1―5：CBCBD 6―10：DCAA
二、填空题（本大题共6小题，每小题5分，共30分）
9． 10． 11．15 12．（1，e） e 13．②③ 14．
三、解答题（本大题共6小题，共80分）
15．（共13分）
解：（I） 令，解得
所以函数的单调递减区间为
（II）因为
所以
因为在（－1，3）上，所以在[－1，2]上单调递增，又由于在
[－2，－1]上单调递减，因此和分别是在区间[－2，2]上的最大值和
最小值.
于是有，解得
故 因此
即函数在区间[－2，2]上的最小值为－7.
解法一：
（Ⅰ）在直四棱柱ABCD―A1B1C1D1中，
∵A1A⊥底面ABCD，
∴AC是A1C在平面ABCD上的射影，
∵BD⊥AC， ∴BD⊥A1C.
（Ⅱ）连结A1E，C1E，A1C1.
与（Ⅰ）同理可证BD⊥A1E，BD⊥C1E，
∴∠A1EC1二面角A1―BD―C1的平面角.
∵AD⊥DC， ∴∠A1D1C1=∠ADC=90°，
又A1D1=AD=2，D1C1=DC=2， AA1=，且AC⊥BD，
∴A1C1=4，AE=1，EC=3， ∴A1E=2，C1E=2，
在△A1EC1中，A1C12=A1E2+C1E2， ∴∠A1EC1=90°，
即二面角A1―BD―C1的大小为90°.
（Ⅲ）过B作BF//AD交AC于F，连结FC1，
则∠C1BF就是AD与BC1所成的角.
∵AB=AD=2，BD⊥AC，AE=1， ∴BF=2，EF=1，FC=2，BC=DC，
∴FC1=. 在△BFC1中，
∴
即异面直线AD与BC1所成角的大小为.
解法二：
（Ⅰ）同解法一.
（Ⅱ）如图，以D为坐标原点，DA，DC，DD1所在直线分别为x轴，y轴，z轴，建立空间直角坐标系.
与（Ⅰ）同理可证，BD⊥A1E，BD⊥C1E，
∴∠A1EC1为二面角A1―BD―C1的平面角.
（Ⅲ）如图，由D（0，0，0），A（2，0，0），C1（0，，，），B（3，，0）
∴异面直线AD与BC1所成角的大小为arccos.
解法三：
（II）如图，建立空间直角坐标系，坐标原点为E.
连结A1E，C1E，A1C1.
与（I）同理可证，BD⊥A1E，BD⊥C1E，
∴∠A1EC1为二面角A1―BD―C1的平面角.
由E（0，0，0），A1（0，－1，
.
（Ⅲ）如图，由A（0，－1，0），D（，0，0），B（，0，0），C1（0，3，）.
得.
∵
∴
∴异面直线AD与BC1所成角的大小为arccos.
17．（共13分）
解：（Ⅰ）
ξ的概率分布如下表：
ξ
0
1
2
3
P
Eξ=0?+1?+2?+3?=1.5 （或Eξ=3?）
（Ⅱ）乙至多击中目标2次的概率为
（Ⅲ）设甲恰比乙多击中目标2次为事件A，甲恰击中目标2次且乙恰击中目标0次为事件B1，甲恰击中目标3次且乙恰击中目标1次为事件B2，则A=B1+B2，B1、B2为互斥事件.
P（A）=P（B1）+P（B2）=
所以，甲恰好比乙多击中目标2次的概率为
18．（共14分）
解：（I）
（II）直线由题意得
（III）当直线l与x轴垂直时，可设直线l的方程为. 由于直线l，曲线C关于x轴对称，且l1与l2关于x轴对称，于是M1M2，M3M4的中点坐标都为（a，0），所以△OM1M2，△OM3M4的重心坐标都为，即它们的重心重合.
当直线l与x轴不垂直时，设直线l的方程为
由
由直线l与曲线C有两个不同交点，可知
于是△OM1M2的重心与△OM3M4的重心也重合.
19．（共12分）
解：（Ⅰ）
（Ⅱ）因为
所以
猜想：是公比为的等比数列.
证明如下： 因为
所以是首项为的等比数列.
（Ⅲ）
20．（共14分）
（Ⅰ）证明：设的峰点，则由单峰函数定义可知，上单调递增，
在上单调递减.
当，
这与是含峰区间.
当
这与是含峰区间.
（II）证明：由（I）的结论可知：
当f(x1)≥f(x2)时，含峰区间的长度为l1=x2；
当f(x1)≤f(x2)时，含峰区间的长度为l2=1－x1；
对于上述两种情况，由题意得
① 由①得1+x2－x1≤1+2r，即x2－x1≤2r.
又因为x2－x1≥2r，所以x2－x1=2r，所以 x2－x1=2r. ②
将②代入①得 x1≤0.5－r, x2≥0.5+r. ③
由①和③解得x1=0.5－r, x2=0.5+r.
所以这时含峰区间的长度l1=l2=0.5+r，即存在x1 , x2使得所确定的含峰区间的长度不大于0.5+r.
（Ⅲ）解：对先选择的x1, x2, x1 <x2， 由（II）可知 x1+x2=1， ④
在第一次确定的含峰区间为（0，x2）的情况下，x3的取值应满足 x3+x1=x2 , ⑤
由④与⑤可得 当x1>x3时，含峰区间的长度为x1.
由条件x1－x3≥0.02, 得x1－(1－2x1) ≥0.02, 从而x1≥0.34.
因此，为了将含峰区间的长度缩短到0.34，只要取
x1=0.34, x2=0.66, x3=0.32.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com