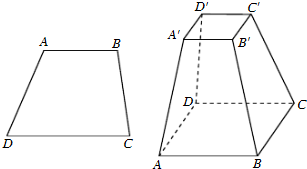（必做题）先阅读：如图，设梯形ABCD的上、下底边的长分别是a，b（a＜b），高为h，求梯形的面积．
方法一：延长DA、CB交于点O，过点O作CD的垂线分别交AB、CD于E、F，则EF=h．
设OE=x，∵△OAB∽△ODC，∴

x

x+h

=

a

b

，即x=

ah

b-a

．
∴S_梯形ABCD=S_△ODC-S_△OAB=

1

2

b（x+h）-

1

2

ax=

1

2

（b-a）x+

1

2

bh=

1

2

（a+b）h．
方法二：作AB的平行线MN分别交AD、BC于MN，过点A作BC的平行线AQ分别于MN、DC于PQ，则△AMP∽△ADQ．
设梯形AMNB的高为x，MN=y，

x

h

=

y-a

b-a

⇒y=a+

b-a

h

x，∴S梯形ABCD=

∫

h 0

（a+

b-a

h

x）dx=（ax+

b-a

2h

x²）

|

h 0

=ah+

b-a

2h

•h²=

1

2

（a+b）h．
再解下面的问题：
已知四棱台ABCD-A′B′C′D′的上、下底面的面积分别是S₁，S₂（S₁＜S₂），棱台的高为h，类比以上两种方法，分别求出棱台的体积（棱锥的体积=

1

3

×底面积×高）．

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

小明做了两道题，事件A为“做对第一个”，事件B为“做对第二个”，其中“做对第一个”与“做对第二个”的概率都是，下列说法正确的是（　　）

    A．小明做对其中一个的概率为

    B．事件A与事件B为互斥事件

    C．A∩B={两个题都做对}

    D．事件A与事件B必然要发生一个

     

查看答案和解析>>

查看答案和解析>>

说明：1．参考答案与评分标准指出了每道题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与参考答案不同，可根据试题主要考查的知识点和能力比照评分标准给以相应的分数．

      2．对解答题中的计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的得分，但所给分数不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．

      3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．

4．只给整数分数，选择题和填空题不给中间分．

一、选择题：本大题考查基本知识和基本运算．共8小题，每小题5分，满分40分．

题号

1

2

3

4

5

6

7

8

答案

A

C

B

C

B

A

D

D

二、填空题：本大题共7小题，每小题5分，满分30分．其中13~15题是选做题，考生只能选做二题，三题全答的，只计算前二题得分．第12题第1个空3分，第2个空2分.

9．2          10．79         11．0 或 2       12．16，

13．1         14．3          15．6

三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．

16．（本小题主要考查三角函数性质和三角函数的基本关系等知识，考查化归与转化的数学思想方法，以及运算求解能力）

解：（1）

                 ．                

∵，

∴函数的值域为．                                     

（2）∵，，∴，．

∵都为锐角，∴，．

∴                    

            ．

∴的值为．                                      

17．（本小题主要考查空间线面关系、几何体的表面积与体积等基本知识，考查数形结合的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力）

解：（1）设,∵几何体的体积为，

∴，                      

即，

即，解得．

∴的长为4．                                           

（2）在线段上存在点，使直线与垂直．     

以下给出两种证明方法：

方法1：过点作的垂线交于点，过点作 

交于点．

∵，，，

∴平面．

∵平面，∴．

∵，∴平面．

∵平面，∴．      

在矩形中，∵∽，

∴，即，∴．

∵∽，∴，即，∴．

在中，∵，∴．

由余弦定理，得

．

∴在线段上存在点,使直线与垂直，且线段的长为．

方法2：以点为坐标原点，分别以，，所在的直线为轴，轴，轴建立如图的空间直角坐标系，由已知条件与（1）可知，，，，  

假设在线段上存在点≤≤2，，0≤≤

使直线与垂直，过点作交于点．

由∽，得，

∴．

∴．

∴，．

∵，∴，

即，∴．       

此时点的坐标为，在线段上．

∵，∴．

∴在线段上存在点，使直线与垂直，且线段的长为．

18．（本小题主要考查等差数列、等比数列的通项公式与前项和公式等基础知识，考查化归与转化、分类与整合的数学思想方法，以及推理论证能力和运算求解能力）

解：设等比数列的首项为，公比为，

若，，成等差数列，

则．

∴．

∵，，∴．

解得或．             

当时，∵，，，         

∴．

∴当时，，，不成等差数列．

当时，，，成等差数列．下面给出两种证明方法．

证法1：∵

                            ，

∴．

∴当时，，，成等差数列．

证法2：∵，          

又

              ， 

∴．

∴当时，，，成等差数列． 

19．（本小题主要考查等可能事件、互斥事件和独立重复试验等基础知识，考查化归与转化的数学思想方法，以及推理论证能力和运算求解能力）

解：（1）∵一次摸球从个球中任选两个，有种选法，                         

任何一个球被选出都是等可能的，其中两球颜色相同有种选法，

∴一次摸球中奖的概率．             

（2）若，则一次摸球中奖的概率，                  

三次摸球是独立重复试验，三次摸球恰有一次中奖的概率是

．                                    

（3）设一次摸球中奖的概率为，则三次摸球恰有一次中奖的概率为，，

∵，

∴在上为增函数，在上为减函数．              

∴当时，取得最大值．

∵≥，

解得．

故当时，三次摸球恰有一次中奖的概率最大．                 

20．（本小题主要考查函数的性质、函数与导数等知识，考查化归与转化、分类与整合的数学思想方法，以及抽象概括能力、推理论证能力和运算求解能力）

（1）解法1：∵，其定义域为，  

∴．                

∵是函数的极值点，∴，即．                                         

∵，∴．                                               

经检验当时，是函数的极值点，

∴．　                                            

解法2：∵，其定义域为，

∴．               

令，即，整理，得．

∵，

∴的两个实根（舍去），，

当变化时，，的变化情况如下表：

―

0

＋

极小值

依题意，，即，

∵，∴．                           

（2）解：对任意的都有≥成立等价于对任意的都有≥．                       

当［1，］时，