练习册

  • 练习册
  • 试题
    . 【查看更多】

     

    题目列表(包括答案和解析)

    10、，设{an}是正项数列，其前n项和Sn满足：4Sn=（an-1）（an+3），则数列{an}的通项公式an=
    2n+1
    ．

    查看答案和解析>>

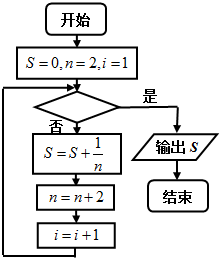    精英家教网，如图给出的是计算
    1
    2
    +
    1
    4
    +
    1
    6
    +…+
    1
    20
    的值的一个程序框图，其中判断框内填入的条件是
     
    ．

    查看答案和解析>>

    5、α，β为两个互相垂直的平面，a、b为一对异面直线，下列条件：
    ①a∥α、b?β；②a⊥α．b∥β；
    ③a⊥α．b⊥β；④a∥α、b∥β且a与α的距离等于b与β的距离，其中是a⊥b的充分条件的有（　　）

    查看答案和解析>>

    ，设f（x）是定义在R上的以3为周期的奇函数，且f（2）=0，则．
    （i）f（
    32
    ）=
     
    ；
    （ii）设S为f（x）=0在区间[0，20]内的所有根之和，则S的最小值为
     
    ．

    查看答案和解析>>

    ，已知y=f（x）是定义在R上的单调递减函数，对任意的实数x，y都有f（x+y）=f（x）f（y）且f（0）=1，数列{an}满足a1=4，f(log3-
    an+1
    4
    )f(-1-log3
    an
    4
    )=1    （n∈N*）．
    （1）求数列{an}的通项公式；
    （2）设Sn是数列{an}的前n项和，试比较Sn与6n2-2的大小．

    查看答案和解析>>

    1－12  BDBDA    BABCABD

    13．?2

    14．2n＋1－n－2

    15．7

    16．90

    17．（1）∵∴.

    （2）证明：由已知，

    故，

    ∴ .

    18．（1）由得，当时，，显然满足，

    ∴，

    ∴数列是公差为4的递增等差数列.

    （2）设抽取的是第项，则，.

    由，

    ∵，∴，

    由.

    故数列共有39项，抽取的是第20项.

    19．。

    ∴

    ∴

    记①

    ②

    ①+②得③

    ，

    ∴

    ∴

    ∴

    ∴

    20．（1）由条件得： .

    （2）假设存在使成立，则    对一切正整数恒成立.

    ∴， 既.

    故存在常数使得对于时，都有恒成立.

    21．（1）第1年投入800万元，第2年投入800×（1－）万元……，

    第n年投入800×（1－）n－1万元，

    所以总投入an＝800＋800（1－）＋……＋800×（1－）n－1＝4000［1－（）n］

    同理：第1年收入400万元，第2年收入400×（1＋）万元，……，

    第n年收入400×（1＋）n－1万元

    bn＝400＋400×（1＋）＋……＋400×（1＋）n－1＝1600×［（）n－1］

    （2）∴bn－an＞0，1600［（）n－1］－4000×［1－（）n］＞0

    化简得，5×（）n＋2×（）n－7＞0

    设x＝（）n，5x2－7x＋2＞0

    ∴x＜，x＞1（舍)，即（）n＜，n≥5.

    22．（文）

    （1）当时，

    由，即 ，

    又.

    （1）

    （2）

    由（1）得

    当

    若成立

    若故所得数列不符合题意.

    当

    若

    若.

    综上，共有3个满足条件的无穷等差数列：

    ①{an} : an=0，即0，0，0，…；

    ②{an} : an=1，即1，1，1，…；

    ③{an} : an=2n－1，即1，3，5，…，

    （理）

    （1）由已知得：，

    ∵，

    ∴或，

    ∴或.

    （2）由，∴，

    ∴，  ∴是等比数列.

    ∵ ，∴ ，

    ∴ ，

    ∵  ，当时，，

    . ，

    故.


    同步练习册答案