已知椭圆E：

x2

a2

+

y2

b2

=1(a＞b＞0)的离心率为

2

2

，且过点P(2，

2

)，设椭圆的右准线l与x轴的交点为A，椭圆的上顶点为B，直线AB被以原点为圆心的圆O所截得的弦长为

4 5

5

．
（1）求椭圆E的方程及圆O的方程；
（2）若M是准线l上纵坐标为t的点，求证：存在一个异于M的点Q，对于圆O上任意一点N，有

MN

NQ

为定值；且当M在直线l上运动时，点Q在一个定圆上．

查看答案和解析>>

已知椭圆E：

x2

a2

+

y2

b2

=1(a＞b＞0)的离心率为

3

3

，它的上顶点为A，左、右焦点分别为F₁，F₂，直线AF₁，AF₂分别交椭圆于点B，C．
（1）求证直线BO平分线段AC；
（2）设点P（m，n）（m，n为常数）在直线BO上且在椭圆外，过P的动直线l与椭圆交于两个不同点M，N，在线段MN上取点Q，满足

MP

NP

=

MQ

QN

，试证明点Q恒在一定直线上．

查看答案和解析>>

已知椭圆E：

x2

a2

+

y2

b2

=1(a＞b＞0)的离心率为

3

3

，它的上顶点为A，左、右焦点分别为F₁，F₂，直线AF₁，AF₂分别交椭圆于点B，C．
（1）求证直线BO平分线段AC；
（2）设点P（m，n）（m，n为常数）在直线BO上且在椭圆外，过P的动直线l与椭圆交于两个不同点M，N，在线段MN上取点Q，满足

MP

NP

=

MQ

QN

，试证明点Q恒在一定直线上．

查看答案和解析>>

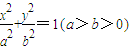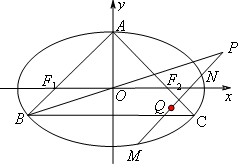
已知椭圆E：的离心率为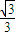，它的上顶点为A，左、右焦点分别为F₁，F₂，直线AF₁，AF₂分别交椭圆于点B，C．
（1）求证直线BO平分线段AC；
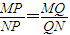（2）设点P（m，n）（m，n为常数）在直线BO上且在椭圆外，过P的动直线l与椭圆交于两个不同点M，N，在线段MN上取点Q，满足，试证明点Q恒在一定直线上．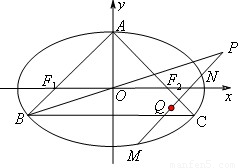

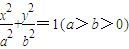查看答案和解析>>

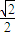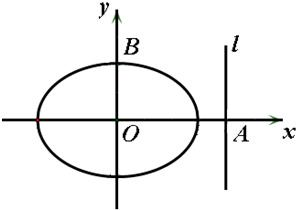
已知椭圆E：的离心率为，且过点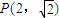，设椭圆的右准线l与x轴的交点为A，椭圆的上顶点为B，直线AB被以原点为圆心的圆O所截得的弦长为．
（1）求椭圆E的方程及圆O的方程；
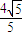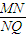（2）若M是准线l上纵坐标为t的点，求证：存在一个异于M的点Q，对于圆O上任意一点N，有为定值；且当M在直线l上运动时，点Q在一个定圆上．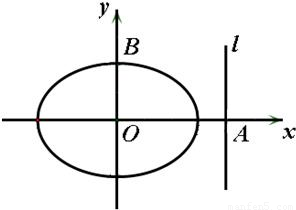

查看答案和解析>>

一、选择题

题号

1

2

3

4

5

6

7

8

9

10

答案

A

A

B

A

D

B

C

B

D

C

二、填空题

11．         12．   【-1，1】    13．      北偏东30度   ，________10___

14．                   15．  60                16．                 

17．___________________

三、简答题

18．（本题14分）（1）a=1     (2)

19．（本题14分）（1）

0

1

2

P

（?）；

（?），当m=5时，取到最大。

   （2）m=5

20．（本题14分）

   （1）

   （2）不存在

21．（本小题满分15分）

   （1）m=1

   （2）（参数法较简单）

22．（本小题满分15分）

   （1）定义域为，

当时，在上是增函数；

当时，在上是减函数，在上是增函数。

   （2）

   （3）