练习册

  • 练习册
  • 试题
    (A) (B) . (C) (D) 【查看更多】

     

    题目列表(包括答案和解析)

    （08年江西卷理）如图1，一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块，容器内盛有升水时，水面恰好经过正四棱锥的顶点P。如果将容器倒置，水面也恰好过点（图2）。有下列四个命题：

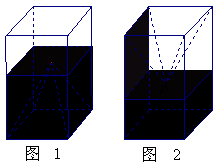
    A．正四棱锥的高等于正四棱柱高的一半

    B．将容器侧面水平放置时，水面也恰好过点

    C．任意摆放该容器，当水面静止时，水面都恰好经过点

    D．若往容器内再注入升水，则容器恰好能装满

    其中真命题的代号是：              （写出所有真命题的代号）．

    查看答案和解析>>

    （08年江西卷理）连结球面上两点的线段称为球的弦。半径为4的球的两条弦、的长度分别等于、，、分别为、的中点，每条弦的两端都在球面上运动，有下列四个命题：

    ①弦、可能相交于点         ②弦、可能相交于点

    ③的最大值为5                    ④的最小值为1

    其中真命题的个数为

    A．1个     B．2个       C．3个       D．4个

    查看答案和解析>>

    （08年长沙一中一模理）某种游戏中，黑、黄两个“电子狗”从棱长为1的正方体的顶点A出发沿棱向前爬行，每爬完一条棱称为“爬完一段”。黑“电子狗”爬行的路线是，黄“电子狗”爬行的路线是它们都遵循如下规则：所爬行的第段与第段所在直线必须是异面直线（其中是正整数）.设黑“电子狗”爬完2008段、黄“电子狗”爬完2007段后知自停止在正方体的某个顶点处，这时黑、黄“电了狗”间的距离是（    ）

           A．0                            B．1                            C．                       D．

    查看答案和解析>>

    （07年全国卷Ⅰ）已知椭圆的左右焦点分别为、，过的直线交椭圆于B、D两点，过的直线交椭圆于A、C两点，且，垂足为P

    （Ⅰ）设P点的坐标为，证明：；

    （Ⅱ）求四边形ABCD的面积的最小值。

    查看答案和解析>>

    （07年上海卷理）已知是定义域为正整数集的函数，对于定义域内任意的，若  成立，则成立，下列命题成立的是

    A、若成立，则对于任意，均有成立；

    B、若成立，则对于任意的，均有成立；

    C、若成立，则对于任意的，均有成立；

    D、若成立，则对于任意的，均有成立。

    查看答案和解析>>

     一、选择题

     

     

     

    二．填空题

    (13)         (14)10；         (15)180；           (16)① ③④

     三．解答题

    (17)(本小题满分10分)

    解 ：

    （Ⅰ）

    函数 的单调增区间为

    （Ⅱ）

     

     

     

     

     (18)(本小题满分12分)

    解：(I)当

     (II)由(I)得

      

         

    (19)(本小题满分12分)

    解：依题意，第四项指标抽检合格的概率为 其它三项指标抽检合格的概率均为

        

        (I)若食品监管部门对其四项质量指标依次进行严格的检测，恰好在第三项指标检测结束

    时，  能确定该食品不能上市的概率等于第一、第二项指标中恰有一项不合格而且第三项指标不合格的概率．

     

     

      (II)该品牌的食品能上市的概率等于四项指标都含格或第一、第二、第三项指标中仅有

    一项不合格且第四项指标合格的概率．

     

    (20)(本小题满分12分)

    解法1：(I)取A1C1中点D，连结B1D，CD．

    C1C=AlA=AlC， CD⊥AlCl．

    底面 ABC是边长为2的正三角形，

    AB=BC=2，A1B1=BlCl=2，

    B1D⊥AlCl．

    又BlDCD=D，A1C1平面B1CD, A1C1B1C

    (II) 面A1ACCl⊥底面ABC，面AlACC1⊥A1BlC1

    又B1D⊥AlC1 BID⊥面A1CCl  

    过点D作DE⊥A1C，连BlE，则BlE⊥AlC

    B1ED为所求二面角的平面角  

     又A1A⊥A1C, C1C⊥A1C,又D是A1C1的中点，

         

      故所求二面角B1一A1C―C1的大小为arctan．

    解法2：(I)取AC中点O，连结BO，   ABC是正三角形 BO⊥AC    

    又面 A1ACC1⊥底面ABC，BO⊥面A1ACC1 , BO⊥OA1

    又AlA=A1C，A1O⊥AC，如图建立空间直角坐标系O一xyz

    则 （Ⅱ）为平面A1B1C的一个法向量，

    ．

     

    故二面角B1-A1C-C1的大小为arccos

    (21)(本小题满分12分)  。

      解：(I)曲线 在点( 0，)处的切线与 轴平行  分

     

         (II)由c=0，方程 可化为

    假没存在实数b使得此方程恰有一个实数根，

    ①

      此方程恰有一个实根

    ②若b>o，则  的变化情况如下

     

     

    ③若b＜o，则  的变化情况如下

     

    综合①②③可得，实数b的取值范围是

     

    （22）解：， （Ⅰ）由题意设双曲线的标准方程为

    由已知得

     

     双曲线G的标准方程为

    （Ⅱ）

     

     

    化简整理得,

    www.ks5u.com

     


    同步练习册答案