
题目列表(包括答案和解析)
 某市中学生田径运动会总分获得冠、亚、季军的代表队人数情况如下表.大会组委会为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插拙奖活动,并用分层抽样的方法从三个代表队中共抽取16人在前排就坐,其中亚军队有5人.
某市中学生田径运动会总分获得冠、亚、季军的代表队人数情况如下表.大会组委会为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插拙奖活动,并用分层抽样的方法从三个代表队中共抽取16人在前排就坐,其中亚军队有5人.名次 性别 | 冠军队 | 亚军队 | 季军队 |
| 男生 | 30 | 30 | * |
| 女生 | 30 | 20 | 30 |
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
(Ⅰ)求n的值;
(Ⅱ)把在前排就坐的高二代表队6人分别记为a、b、c、d、e、f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率;
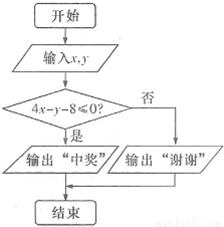
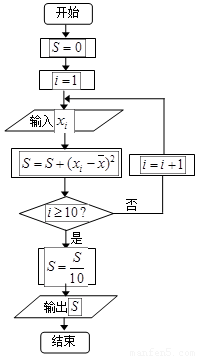
(Ⅲ)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x、y,并按如下所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
在每年的春节后,某市政府都会发动公务员参与到植树活动中去.为保证树苗的质量,该市林管部门在植树前,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出树苗的高度如下(单位:厘米):
甲: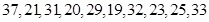
乙: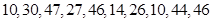
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;
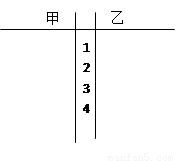
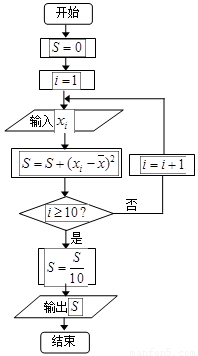
(2)设抽测的10株甲种树苗高度平均值为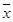 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的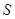 大小为多少?并说明
大小为多少?并说明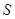 的统计学意义.
的统计学意义.
在每年的春节后,某市政府都会发动公务员参与到植树活动中去.为保证树苗的质量,该市林管部门在植树前,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出树苗的高度如下(单位:厘米):
甲:
乙: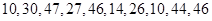
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;
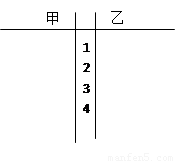
(2)设抽测的10株甲种树苗高度平均值为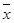 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的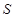 大小为多少?并说明
大小为多少?并说明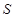 的统计学意义.
的统计学意义.
在每年的春节后,某市政府都会发动公务员参与到植树活动中去.为保证树苗的质量,该市林管部门在植树前,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出树苗的高度如下(单位:厘米):
甲:
乙:
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的10株甲种树苗高度平均值为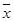 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的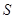 大小为多少?并说明
大小为多少?并说明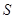 的统计学意义.
的统计学意义.
一、选择题:本题考查基础知识和基本运算. 每题5分,满分60分.
1.D 2。C 3.C 4.A 5.B 6.D
7.A 8.B 9.A 10.C 11.B 12.A
二、填空题:本题考查基础知识和基本运算. 每题4分,满分16分.
13.15 14.4 15 . 16
16 
三、解答题:本题共6大题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.本题主要考查三角函数性质、三角恒等变换等基本知识,考查推理和运算能力.
解:( I )

(Ⅱ)

18.本题主要考查简单随机抽样,用古典概型计算事件发生的概率等基础知识,考查研究基本事件的能力,以及应用意识。
解:(I)设红色球有 个,依题意得
个,依题意得 红色球有4个.
红色球有4个.
(II)记“甲取出的球的编号比乙的大”为事件A
所有的基本事件有(红1,白1),(红l,蓝2),(红1,蓝3),(白l,红1),
(白1,蓝2),(白1,蓝3),(蓝2,红1),(蓝2,自1),(蓝2,蓝3),
(蓝3,红1),(蓝3,白1),(蓝3,蓝2),共12个
事件A包含的基本事件有(蓝2,红1),(蓝2,白1),
(蓝3,蓝2),共5个
所以,

19.本题主要考查线面平行与垂直关系,及多面体的体积计算等基础知识,考查空间想象能力,逻辑思维能力和运算能力.
(I)解:取CD的中点为F,连EF,则EF为 的中位线.
的中位线.
 EF∥A
EF∥A
又EF  平面A1BC,.
平面A1BC,. EF∥平面A1BC
EF∥平面A1BC
 (II)证:四边形ABCD为直角梯形且AD∥BC,
(II)证:四边形ABCD为直角梯形且AD∥BC,
AB⊥BC,AD=2,AB=_BC=1. AC=CD=
AC=CD=  ,
,
 AD2=AC2+CD2 即
AD2=AC2+CD2 即 为直角三角形 CD⊥AC又四棱 柱ABCD一A1B
为直角三角形 CD⊥AC又四棱 柱ABCD一A1B
CD  底面ABCD
底面ABCD  AAl⊥CD,又AA1与AC交于点A,
AAl⊥CD,又AA1与AC交于点A,
 CD⊥平面A1ACCl
CD⊥平面A1ACCl
由CD⊥平面AlACCl, CD为四棱锥D-A1ACCl的底面 A1ACCl上的高,
CD为四棱锥D-A1ACCl的底面 A1ACCl上的高,
又AAl垂直于底面ABCD, 四边形A1ACC1为矩形
四边形A1ACC1为矩形
 四棱锥D―A1ACCI的体积
四棱锥D―A1ACCI的体积
20.此题主要考查数列、等差、等比数列的概念、数列的递推公式、数列前n项和的求法
同时考查学生的分析问题与解决问题的能力,逻辑推理能力及运算能力.
解:(I)

(Ⅱ)
 21.本题主要考查直线方程与性质、椭圆方程与性质以及直线与曲线的位置关系等基础知
21.本题主要考查直线方程与性质、椭圆方程与性质以及直线与曲线的位置关系等基础知
识;考查考生数形结合思想、运算求解能力、推理论证能力。
解:(I)

(Ⅱ)

22.本题主要考查二次函数及其性质、导数的基本知识,几何意义及其应用,同时考查考生分类讨论思想方法及化规的能力:
解:(Ⅰ)

(Ⅱ)

(Ⅲ)

① 

② 
③ 

方程 有两个不等的正根,存在两条满足条件的切线;
有两个不等的正根,存在两条满足条件的切线;


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com