
题目列表(包括答案和解析)
| y2 |
| a2 |
| x2 |
| b2 |
| 3 |
| y2 |
| a2 |
| x2 |
| b2 |
| 3 |
| 2 |
已知椭圆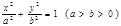 和圆
和圆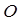 :
: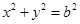 ,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
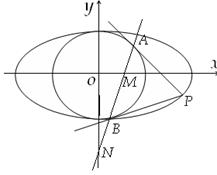
(1)(ⅰ)若圆O过椭圆的两个焦点,求椭圆的离心率e的值;
(ⅱ)若椭圆上存在点P,使得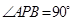 ,求椭圆离心率e的取值范围;
,求椭圆离心率e的取值范围;
(2)设直线AB与x轴、y轴分别交于点M,N,问当点P在椭圆上运动时,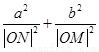 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.
已知椭圆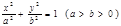 和圆
和圆 :
: ,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
,过椭圆上一点P引圆O的两条切线,切点分别为A,B. 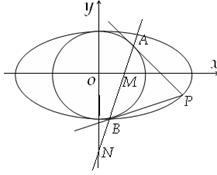
(1)(ⅰ)若圆O过椭圆的两个焦点,求椭圆的离心率e的值;
(ⅱ)若椭圆上存在点P,使得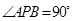 ,求椭圆离心率e的取值范围;
,求椭圆离心率e的取值范围;
(2)设直线AB与x轴、y轴分别交于点M,N,问当点P在椭圆上运动时,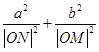 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.
 .
. 为圆O:
为圆O: 的弦AB的中点,则直线AB的斜率
的弦AB的中点,则直线AB的斜率 与直线OE的斜率
与直线OE的斜率 的乘积
的乘积 为定值。类比圆的这个性质,写出椭圆
为定值。类比圆的这个性质,写出椭圆 的类似性质,并加以证明;
的类似性质,并加以证明; 在第一象限中的任意一点,过B作
在第一象限中的任意一点,过B作 的切线
的切线 ,
, 分别与x轴和y轴的正半轴交于C,D两点,求三角形OCD面积的最小值;
分别与x轴和y轴的正半轴交于C,D两点,求三角形OCD面积的最小值; 上任意一点
上任意一点 作
作 的两条切线PM和PN,切点分别为M,N.当点P在椭圆
的两条切线PM和PN,切点分别为M,N.当点P在椭圆 上运动时,是否存在定圆恒与直线MN相切?若存在,求出圆的方程;若不存在,请说明理由.
上运动时,是否存在定圆恒与直线MN相切?若存在,求出圆的方程;若不存在,请说明理由.

 的左顶点A和上顶点D,椭圆C的右顶点为B,点P是椭圆C上位于x轴上方的动点,直线AP,BP与直线l:x=5分别交于M,N两点.
的左顶点A和上顶点D,椭圆C的右顶点为B,点P是椭圆C上位于x轴上方的动点,直线AP,BP与直线l:x=5分别交于M,N两点.一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
B
A
D
B
C
C
D
D
A
C
二、填空题
13..files/image206.gif) 14.
14..files/image208.gif) 15.4 16.③④
15.4 16.③④
三、解答题
17.解:(1)∵.files/image210.gif) ,
,.files/image212.gif) ,
,
∴.files/image214.gif) .
…………2分
.
…………2分
又.files/image216.gif) , …………4分
, …………4分
∴.files/image218.gif) ,∴
,∴.files/image220.gif) .
…………6分
.
…………6分
(2)∵.files/image222.gif) ,
,.files/image148.gif) ,
,.files/image218.gif) ,
,
∴.files/image225.gif) . …………8分
. …………8分
∵.files/image227.gif) ,
,
.files/image228.gif) ∴
∴.files/image230.gif) .
.
∴.files/image232.gif) ,
,
∴.files/image234.gif) .…………10分
.…………10分
18.(1)证明:连结BD交AC于点M,取BE的中点N,
连结MN,则MN∥ED且MN=.files/image236.gif) ED,依题意,
ED,依题意,
知AG∥ED且AG=.files/image236.gif) ED,
ED,
∴MN∥AG且MN=AG.
故四边形MNAG是平行四边形, AM∥GN,
即AC∥GN,…………3分
又∵.files/image238.gif)
∴ AC∥平面GBE.…………6分
(2)解:延长EG交DA的延长线于H点,
连结BH,作AO⊥GH于O点,连结BO.
∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,AB⊥AD
∴ AB⊥平面ADEF,由三垂线定理,知AB⊥GH,
故∠AOB就是二面角B-GE-D的平面角.…………8分
∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,ED⊥AD
∴ ED⊥平面ABCD,
故∠EBD就是直线BE与平面ABCD成的角,……10分
知∠EBD=45°,设AB=a,则BE=BD=.files/image240.gif) a.
a.
在直角三角形AGH中:AH=AD= a,AG=.files/image242.gif) =
=.files/image244.gif) a,
a,
HG=.files/image246.gif) ,AO=
,AO=.files/image248.gif) .
.
在直角三角形ABO中:tan∠AOB=.files/image250.gif) .
.
∴ ∠AOB=60°.
故二面角B-GE-D的大小为60°.…………12分
19.解:(1)记A0表示事件“取出的2件产品中无二等品”,A1表示事件“取出的2件产品中恰有1件是二等品”.则A0、A1互斥,且A=A0+A1.
故P (A)=P (A0+A1)=P
(A0) +P (A1)=(1-p)2+C.files/image252.gif) p (1-p)=1-p2.
p (1-p)=1-p2.
依题意,知1-p2=0.96,又p>0,得p=0.2.…………6分
(2)(理)ξ可能的取值为0,1,2.
若该批产品共100件,由(1)知,其中共有二等品100×0.2=20件,故
P(ξ=0)=.files/image254.gif) .P(ξ=1)=
.P(ξ=1)=.files/image256.gif) .
.
P(ξ=2)=.files/image258.gif) .…………9分
.…………9分
所以ξ的分布列为
ξ
0
1
2
P
.files/image260.gif)
.files/image262.gif)
.files/image264.gif)
.files/image266.gif) ξ的期望
ξ的期望.files/image268.gif) …………12分
…………12分
20.解 (1).files/image270.gif) 在
在.files/image272.gif) 上单调递增,
上单调递增,.files/image274.gif) 上单调递减,
上单调递减,
.files/image276.gif) 有两根
有两根.files/image278.gif) ,
,
.files/image280.gif) ……4分
……4分
令.files/image282.gif) ,
,
则.files/image284.gif) ,
,
因为.files/image286.gif) 在
在.files/image288.gif) 上恒大于0,所以
上恒大于0,所以.files/image290.gif) 在
在.files/image288.gif) 上单调递增,
上单调递增,
故.files/image292.gif) ,
, .files/image294.gif) ,
,
.files/image296.gif) .
……………6分
.
……………6分
(2).files/image298.gif) ,
,
.files/image300.gif) .
.
.files/image302.gif) .
………………8分
.
………………8分
①当.files/image304.gif) 时,
时,.files/image306.gif) ,定义域为
,定义域为.files/image308.gif) ,
,
.files/image310.gif) 恒成立,
恒成立,.files/image312.gif) 上单调递增;
…………9分
上单调递增;
…………9分
②当.files/image314.gif) 时,
时,.files/image316.gif) ,定义域:
,定义域:.files/image318.gif) ,
,
.files/image310.gif) 恒成立,
恒成立,.files/image321.gif) 上单调递增; …………10分
上单调递增; …………10分
③当.files/image323.gif) 时,
时,.files/image325.gif) ,定义域:
,定义域:.files/image318.gif) ,
,
由.files/image310.gif) 得
得.files/image327.gif) ,由
,由.files/image329.gif) 得
得.files/image331.gif) .
.
故在.files/image333.gif) 上单调递增;在
上单调递增;在.files/image335.gif) 上单调递减. …………11分
上单调递减. …………11分
所以当.files/image304.gif) 时,
时,.files/image312.gif) 上单调递增,故
上单调递增,故.files/image337.gif) 无极值;
无极值;
当.files/image314.gif) 时,
时,.files/image321.gif) 上单增;故
上单增;故.files/image337.gif) 无极值.
无极值.
当.files/image323.gif) 时,
时,.files/image337.gif) 在
在.files/image333.gif) 上单调递增;在
上单调递增;在.files/image335.gif) 上单调递减.
上单调递减.
故.files/image337.gif) 有极小值,且
有极小值,且.files/image337.gif) 的极小值为
的极小值为.files/image341.gif) . …12分
. …12分
21.解:(I)设.files/image343.gif) 依题意得
依题意得
.files/image345.gif) …………2分
…………2分
消去.files/image347.gif) ,整理得
,整理得.files/image349.gif) .…………4分
.…………4分
当.files/image351.gif) 时,方程表示焦点在
时,方程表示焦点在.files/image353.gif) 轴上的椭圆;
轴上的椭圆;
当.files/image355.gif) 时,方程表示焦点在
时,方程表示焦点在.files/image357.gif) 轴上的椭圆;
轴上的椭圆;
当.files/image359.gif) 时,方程表示圆. …………6分
时,方程表示圆. …………6分
(II)当.files/image361.gif) 时,方程为
时,方程为.files/image363.gif) ,
,
设直线.files/image093.gif) 的方程为
的方程为.files/image366.gif) ,
,
.files/image368.gif) …………8分
…………8分
消去.files/image353.gif) 得
得.files/image371.gif) .…………10分
.…………10分
根据已知可得.files/image373.gif) ,故有
,故有.files/image375.gif) ,
,
.files/image377.gif) ,
,
.files/image266.gif) 直线
直线.files/image093.gif) 的斜率为
的斜率为.files/image381.gif) . …………12分
. …………12分
22.证明 (Ⅰ)即证.files/image383.gif) .
.
.files/image385.gif)
.files/image387.gif) ,
,.files/image389.gif) ,
,.files/image391.gif) ,
,
.files/image266.gif)
.files/image394.gif) .…………2分
.…………2分
假设.files/image396.gif) ,则
,则
.files/image398.gif) ,…………4分
,…………4分
.files/image400.gif) ,
,
.files/image266.gif)
.files/image403.gif) .
.
综上所述,根据数学归纳法,命题成立. …………6分
(Ⅱ)由(Ⅰ),得
.files/image405.gif) ,…………8
,…………8
.files/image266.gif)
.files/image408.gif) .…………10
.…………10
又 .files/image410.gif) ,
,.files/image266.gif)
.files/image413.gif) ,
,
即.files/image415.gif) .………12分
.………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com