
题目列表(包括答案和解析)



 的通项公式;
的通项公式; ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 为首项,公比为
为首项,公比为 的数列
的数列 ,
, ,使得数列
,使得数列 中每一项都是数列
中每一项都是数列 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由
的通项公式;若不存在,说明理由数列![]() 的通项公式
的通项公式![]()
![]()
(1)求:f(1)、f(2)、f(3)、f(4)的值;
(2)由上述结果推测出计算f(n)的公式,并用数学归纳法加以证明.
设数列![]() 的通项公式为
的通项公式为![]() 。数列
。数列![]() 定义如下:对于正整数m,
定义如下:对于正整数m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若![]() ,求b3; (2)若
,求b3; (2)若![]() ,求数列
,求数列![]() 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
设数列![]() 的通项公式为
的通项公式为![]() 。数列
。数列![]() 定义如下:对于正整数m,
定义如下:对于正整数m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。
成立的所有n中的最小值。
(1)若![]() ,求b3;
,求b3;
(2)若![]() ,求数列
,求数列![]() 的前2m项和公式;
的前2m项和公式;
(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
设数列 的通项公式为
的通项公式为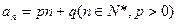 。数列
。数列 定义如下:对于正整数m,
定义如下:对于正整数m, 是使得不等式
是使得不等式 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若 ,求b3; (2)若
,求b3; (2)若 ,求数列
,求数列 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得 ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
一、选择题
题号
1
2
3
4
5
6
7
8
答案
D
A
B
C
B
B
B
D
二、填空题
9.1; 10.(3月).files/image188.gif) ; 11.12; 12.
; 11.12; 12.(3月).files/image190.gif) ; 13.
; 13.(3月).files/image192.gif) ; 14.
; 14.(3月).files/image194.gif)
三、解答题
15.解:(Ⅰ)由(3月).files/image196.gif) ,根据正弦定理得
,根据正弦定理得(3月).files/image198.gif) ,
,
所以(3月).files/image200.gif) ,…………………………………………………………………………………………4分
,…………………………………………………………………………………………4分
由(3月).files/image202.gif) 为锐角三角形得
为锐角三角形得(3月).files/image204.gif) .
…………………………………………7分
.
…………………………………………7分
(Ⅱ)根据余弦定理,得(3月).files/image206.gif)
(3月).files/image208.gif)
(3月).files/image210.gif) .
………10分
.
………10分
所以,(3月).files/image212.gif) .
……………………………………………………………12分
.
……………………………………………………………12分
16.解:(1)由题意可知
当(3月).files/image214.gif) 时,
时,(3月).files/image216.gif) . ……3分
. ……3分
当(3月).files/image218.gif) 时,
时,(3月).files/image220.gif) ,亦满足上式. ……5分
,亦满足上式. ……5分
∴数列(3月).files/image042.gif) 的通项公式为
的通项公式为(3月).files/image223.gif) (
((3月).files/image225.gif) ). ……6分
). ……6分
(2)由(1)可知(3月).files/image227.gif) ,
……7分
,
……7分
∴数列(3月).files/image229.gif) 是以首项为
是以首项为(3月).files/image231.gif) ,公比为
,公比为(3月).files/image233.gif) 的等比数列, ……9分
的等比数列, ……9分
∴(3月).files/image235.gif) .
……12分
.
……12分
(3月).files/image237.jpg) 17.
17.
|