
题目列表(包括答案和解析)
| bx-a | x+2 |
(从22/23/24三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分. 请将答题的过程写在答题卷中指定的位置)(本小题满分10分)选修4—4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的 轴的正半轴重合.直线
轴的正半轴重合.直线 的参数方程是
的参数方程是 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)求曲线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线 与曲线
与曲线 相交于
相交于 ,
, 两点,求M,N两点间的距离.
两点,求M,N两点间的距离.
有以下四个命题:
①对于任意不为零的实数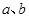 ,有+≥2;
,有+≥2;
②设 是等差数列
是等差数列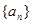 的前
的前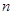 项和,若
项和,若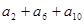 为一个确定的常数,则
为一个确定的常数,则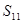 也是一个确定的常数;
也是一个确定的常数;
③关于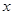 的不等式
的不等式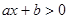 的解集为
的解集为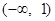 ,则关于
,则关于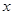 的不等式
的不等式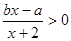 的解集为
的解集为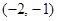 ;
;
④对于任意实数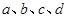 ,
,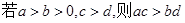 .
.
其中正确命题的是_______________(把正确的答案题号填在横线上)
(从22/23/24三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分. 请将答题的过程写在答题卷中指定的位置)(本小题满分10分)选修4—5:不等式选讲
设函数 .
.
(Ⅰ)求不等式 的解集;
的解集;
(Ⅱ)若不等式 的解集是非空的集合,求实数
的解集是非空的集合,求实数 的取值范围.
的取值范围.
有以下四个命题: ①对于任意实数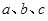 ,
,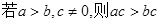 ;
;
②设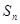 是等差数列
是等差数列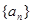 的前
的前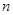 项和,若
项和,若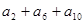 为一个确定的常数,则
为一个确定的常数,则 也是一个确定的常数;③关于
也是一个确定的常数;③关于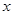 的不等式
的不等式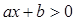 的解集为
的解集为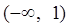 ,则关于
,则关于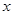 的不等式
的不等式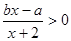 的解集为
的解集为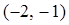 ;④对于任意实数
;④对于任意实数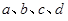 ,
,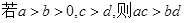 .
.
其中正确命题的是_______________(把正确的答案题号填在横线上)
一、选择题
题号
1
2
3
4
5
6
7
8
答案
D
A
B
C
B
B
B
D
二、填空题
9.1; 10.(3月).files/image188.gif) ; 11.12; 12.
; 11.12; 12.(3月).files/image190.gif) ; 13.
; 13.(3月).files/image192.gif) ; 14.
; 14.(3月).files/image194.gif)
三、解答题
15.解:(Ⅰ)由(3月).files/image196.gif) ,根据正弦定理得
,根据正弦定理得(3月).files/image198.gif) ,
,
所以(3月).files/image200.gif) ,…………………………………………………………………………………………4分
,…………………………………………………………………………………………4分
由(3月).files/image202.gif) 为锐角三角形得
为锐角三角形得(3月).files/image204.gif) .
…………………………………………7分
.
…………………………………………7分
(Ⅱ)根据余弦定理,得(3月).files/image206.gif)
(3月).files/image208.gif)
(3月).files/image210.gif) .
………10分
.
………10分
所以,(3月).files/image212.gif) .
……………………………………………………………12分
.
……………………………………………………………12分
16.解:(1)由题意可知
当(3月).files/image214.gif) 时,
时,(3月).files/image216.gif) . ……3分
. ……3分
当(3月).files/image218.gif) 时,
时,(3月).files/image220.gif) ,亦满足上式. ……5分
,亦满足上式. ……5分
∴数列(3月).files/image042.gif) 的通项公式为
的通项公式为(3月).files/image223.gif) (
((3月).files/image225.gif) ). ……6分
). ……6分
(2)由(1)可知(3月).files/image227.gif) ,
……7分
,
……7分
∴数列(3月).files/image229.gif) 是以首项为
是以首项为(3月).files/image231.gif) ,公比为
,公比为(3月).files/image233.gif) 的等比数列, ……9分
的等比数列, ……9分
∴(3月).files/image235.gif) .
……12分
.
……12分
(3月).files/image237.jpg) 17.
17.
|