
题目列表(包括答案和解析)
(本大题满分14分)
已知数列{an}的前n项和Sn是二项式![]() 展开式中含x奇次幂的系数和.
展开式中含x奇次幂的系数和.
(1)求数列{an}的通项公式;
(2)设![]() ,求
,求![]() ;
;
(3)证明:![]() .
.
(本小题满分14分)
已知数列
(1)计算x2,x3,x4的值;
(2)试比较xn与2的大小关系;
(3)设 ,Sn为数列{an}前n项和,求证:当
,Sn为数列{an}前n项和,求证:当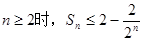 .
.
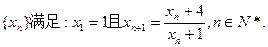
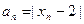 ,Sn为数列{an}前n项和,求证:当
,Sn为数列{an}前n项和,求证:当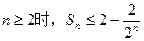 .
.(本题满分14分)
(理)已知数列{an}的前n项和 ,且
,且 =1,
=1,
 .
.
(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有
< f’(x)”.若且函数y=xn+1 在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
(III)求证: ≤bn<2.
≤bn<2.
(本题满分14分)
(理)已知数列{an}的前n项和 ,且
,且 =1,
=1,
 .(I)求数列{an}的通项公式;
.(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有
< f’(x)”.若且函数y=xn+1 在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
(III)求证:≤bn<2.
一.选择题:DCBBA
二.填空题:11.4x-3y-17 = 0 12.33 13.
14. 15.
15.
三.解答题:
16.(1)解:∵ ,
, 2分
2分
∴由 得:
得: ,即
,即 4分
4分
又∵ ,∴
,∴ 6分
6分
(2)解: 8分
8分
由 得:
得: ,即
,即 10分
10分
两边平方得: ,∴
,∴ 12分
12分
 17.方法一
17.方法一
(1)证:∵CD⊥AB,CD⊥BC,∴CD⊥平面ABC 2分
又∵CDÌ平面ACD,∴平面ACD⊥平面ABC 4分
(2)解:∵AB⊥BC,AB⊥CD,∴AB⊥平面BCD,故AB⊥BD
∴∠CBD是二面角C-AB-D的平面角
6分
∵在Rt△BCD中,BC = CD,∴∠CBD = 45°
即二面角C-AB-D的大小为45°
8分
(3)解:过点B作BH⊥AC,垂足为H,连结DH
∵平面ACD⊥平面ABC,∴BH⊥平面ACD,
∴∠BDH为BD与平面ACD所成的角
10分
设AB = a,在Rt△BHD中, ,
,
∴
又 ,∴
,∴ 12分
12分
 方法二
方法二
(1)同方法一 4分
(2)解:设以过B点且∥CD的向量为x轴, 为y轴和z轴建立如图所示的空间直角坐标系,设AB = a,则A(0,0,a),C(0,1,0),D(1,1,0),
为y轴和z轴建立如图所示的空间直角坐标系,设AB = a,则A(0,0,a),C(0,1,0),D(1,1,0), = (1,1,0),
= (1,1,0), = (0,0,a)
= (0,0,a)
平面ABC的法向量 = (1,0,0)
= (1,0,0)
设平面ABD的一个法向量为n = (x,y,z),则

取n = (1,-1,0)
6分

∴二面角C-AB-D的大小为45° 8分
(3)解: = (0,1,-a),
= (0,1,-a), = (1,0,0),
= (1,0,0), = (1,1,0)
= (1,1,0)
设平面ACD的一个法向量是m = (x,y,z),则
∴可取m = (0,a,1),设直线BD与平面ACD所成角为 ,则向量
,则向量 、m的夹角为
、m的夹角为
故 10分
10分
即
又 ,∴
,∴ 12分
12分
18.解:该商场应在箱中至少放入x个其它颜色的球,获得奖金数为 ,
,
则 = 0,100,150,200
= 0,100,150,200
 ,
, ,
,
 ,
, 8分
8分
∴ 的分布列为
的分布列为
|