
题目列表(包括答案和解析)
设 是数列
是数列 的前
的前 项和,对任意
项和,对任意 都有
都有 成立, (其中
成立, (其中 、
、 、
、 是常数).
是常数).
(1)当 ,
, ,
, 时,求
时,求 ;
;
(2)当 ,
, ,
, 时,
时,
①若 ,
,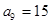 ,求数列
,求数列 的通项公式;
的通项公式;
②设数列 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“ 数列”.
数列”.
如果 ,试问:是否存在数列
,试问:是否存在数列 为“
为“ 数列”,使得对任意
数列”,使得对任意 ,都有
,都有
 ,且
,且 .若存在,求数列
.若存在,求数列 的首项
的首项 的所
的所
有取值构成的集合;若不存在,说明理由.
设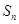 是数列
是数列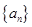 的前
的前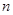 项和,对任意
项和,对任意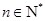 都有
都有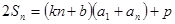 成立, (其中
成立, (其中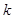 、
、 、
、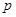 是常数).
是常数).
(1)当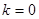 ,
,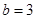 ,
,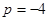 时,求
时,求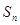 ;
;
(2)当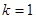 ,
,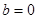 ,
,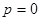 时,
时,
①若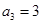 ,
,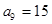 ,求数列
,求数列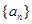 的通项公式;
的通项公式;
②设数列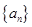 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“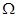 数列”.
数列”.
如果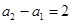 ,试问:是否存在数列
,试问:是否存在数列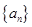 为“
为“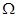 数列”,使得对任意
数列”,使得对任意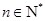 ,都有
,都有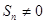 ,且
,且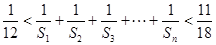 .若存在,求数列
.若存在,求数列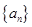 的首项
的首项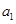 的所
的所
有取值构成的集合;若不存在,说明理由.
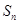 是数列
是数列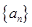 的前
的前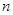 项和,对任意
项和,对任意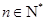 都有
都有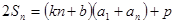 成立, (其中
成立, (其中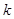 、
、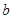 、
、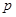 是常数).
是常数).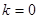 ,
,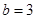 ,
,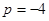 时,求
时,求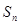 ;
;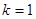 ,
,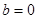 ,
,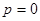 时,
时,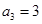 ,
,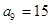 ,求数列
,求数列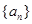 的通项公式;
的通项公式;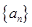 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“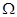 数列”.
数列”.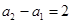 ,试问:是否存在数列
,试问:是否存在数列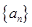 为“
为“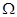 数列”,使得对任意
数列”,使得对任意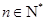 ,都有
,都有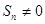 ,且
,且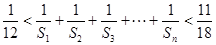 .若存在,求数列
.若存在,求数列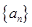 的首项
的首项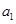 的所
的所设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .数列
.数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)写出一个正整数![]() ,使得
,使得![]() 是数列
是数列![]() 的项;
的项;
(3)设数列![]() 的通项公式为
的通项公式为![]() ,问:是否存在正整数
,问:是否存在正整数![]() 和
和![]() (
(![]() ),使得
),使得![]() ,
,![]() ,
,![]() 成等差数列?若存在,请求出所有符合条件的有序整数对
成等差数列?若存在,请求出所有符合条件的有序整数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
设数列![]() 的通项公式为
的通项公式为![]() 。数列
。数列![]() 定义如下:对于正整数m,
定义如下:对于正整数m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若![]() ,求b3; (2)若
,求b3; (2)若![]() ,求数列
,求数列![]() 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
一. 每小题5分,共60分 DACDB DACBB DD
二. 每小题5分,共20分.其中第16题前空2分,后空3分.
13.
60;
14.  ; 15.
; 15.  ; 16. 2,-
; 16. 2,-
三.解答题:本大题共6个小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(Ⅰ)
∴


(Ⅱ) (7分)
(7分)
 (8分)
(8分)
∴ (10分)
(10分)
18.解:(Ⅰ)记“该人被录用”的事件为事件A,其对立事件为 ,则
,则


(Ⅱ)该生参加测试次数ξ的可能取值为2,3,4,依题意得
|