
题目列表(包括答案和解析)
已知函数
(I)求f(x)在[0,1]上的极值;
(II)若对任意 成立,求实数a的取值范围;
成立,求实数a的取值范围;
(III)若关于x的方程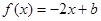 在[0,1]上恰有两个不同的实根,求实数b的取值范围.
在[0,1]上恰有两个不同的实根,求实数b的取值范围.
已知函数![]()
(I)求f(x)在[0,1]上的极值;
(II)若对任意![]() 成立,求实数a的取值范围;
成立,求实数a的取值范围;
(III)若关于x的方程![]() 在[0,1]上恰有两个不同的实根,求实数b的取值范围.
在[0,1]上恰有两个不同的实根,求实数b的取值范围.
已知函数![]()
(I)求f(x)在[0,1]上的极值;
(II)若对任意![]() 成立,求实数a的取值范围;
成立,求实数a的取值范围;
(III)若关于x的方程![]() 在[0,1]上恰有两个不同的实根,求实数b的取值范围.
在[0,1]上恰有两个不同的实根,求实数b的取值范围.
已知函数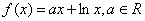 。
。
(I)求函数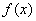 的极值;
的极值;
(II)对于曲线上的不同两点P1(x1,y1),P2(x2,y2),如果存在曲线上的点Q(x0,y0), 且x1<x0<x2,使得曲线在点Q处的切线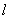 //P1P2,,则称
//P1P2,,则称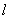 为弦P1P2,的伴随切线。
为弦P1P2,的伴随切线。
特别地,当x0 = 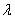 x1 + (1-
x1 + (1-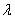 )x2
(0<
)x2
(0<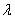 <1)时,又称
<1)时,又称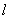 为弦P1P2,的
为弦P1P2,的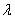 -伴随切线。
-伴随切线。
(i)求证:曲线y=f(x)的任意一条弦均有伴随切线,并且伴随切线是唯一的;
(ii)是否存在曲线C,使得曲线C的任意一条弦均有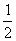 -伴随切线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由。
-伴随切线?若存在,给出一条这样的曲线,并证明你的结论;若不存在,说明理由。

 成立,求实数a的取值范围;
成立,求实数a的取值范围; 在[0,1]上恰有两个不同的实根,求实数b的取值范围.
在[0,1]上恰有两个不同的实根,求实数b的取值范围.一、选择题:
1―5 ACBBD 6―10 BCDAC
二、填空题:
11.60 12. 13.―
13.― 14.
14.
15.2 16. 17.
17.
三、解答题:
18.解:(I)
|