阅读下列各小题，根据括号内的汉语提示，用句末括号内的英语单词完成句子，并将答案写在答题卡上的相应题号后。

71. The minute the shopping mall opens, the customers came___________.( crow )

   购物中心一开业，顾客们便蜂拥而入.

72. We’d like to know ________________________ a businessman like your age has succeeded in remaining energetic. (it)

我想知道一个你这样年龄的商人究竟怎样成功地保持精力充沛。

73. 1 finally got the job I dreamed about．Never in all my life ________________________ so happy. (feel)

我最终找到了我梦想的工作。我一生从来没有这样高兴过。

74. But for the help of my English teacher, I ________________________ in the English Writing Competition. (win)

要不是我的英语老师的帮助，我就不会在英语写作比赛中获得一等奖。

75. The town has changed beyond recognition; now it is _____________what it was 20 years ago.( size )

这座小镇已经变得面目全非了；现在它是20年前的五倍大。

76. The boy, like many other English learners,________________________ in learning English during the past seven years. (meet)

和许多其他英语学习者一样，在过去7年中，那个男孩学习英语遇到了很多困难。

77. ________________________ a heavy traffic jam while you are hurrying to the airport is quite an unpleasant experience. (catch)

赶往机场时，遭遇交通堵塞是很不快的经历。

78. As the College Entrance Examination is in sight, we teachers feel _____________________ you students. (relax)

高考临近，我们老师并不比你们学生感到轻松。

79. It is the lack of movement, along with fatty diets, ________ putting on weight in most people.( lead)

你简直难以想象他在这么短的时间内取得了多么大的进步！

80. Distant education is playing a more and more important role, ____________for people to be educated wherever they are. ( make )

   远程教育正起着越来越重要的作用，这使得人们不管在哪儿都能接受教育。

（本题12分）已知某种从太空带回的植物种子每粒成功发芽的概率都为，某植物研究所分两个小组分别独立开展该种子的发芽实验，每次实验种一粒种子，假定某次实验种子发芽则称该次实验是成功的，如果种子没有发芽，则称该次实验是失败的．

(1) 第一小组做了三次实验，求实验成功的平均次数；

(2) 第二小组连续进行实验，求实验首次成功时所需的实验次数的期望；

(3)两个小组分别进行2次试验，求至少有2次实验成功的概率．

已知关于的方程有实根，复数，则复数在复平面内的对应点到原点的距离为

A．2                B．4             C．            D． 8

已知命题“若函数在是增函数，则”，则下列结论正确的是

A．否命题是“若函数在是减函数，则”，是真命题

B. 逆命题是“若，则函数在是增函数”， 是假命题

C. 逆否命题是“若，则函数在是减函数”， 是真命题

D. 逆否命题是“若，则函数在不是增函数”， 是真命题

已知函数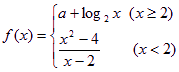在点处连续，则常数的值是

A．2                B．3            C．4               D．5