
题目列表(包括答案和解析)
C.选修4-4:坐标系与参数方程
在极坐标系下,已知圆O: 和直线
和直线 ,
,
(1)求圆O和直线 的直角坐标方程;(2)当
的直角坐标方程;(2)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
D.选修4-5:不等式证明选讲
对于任意实数
 和
和 ,不等式
,不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
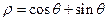 和直线
和直线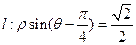 ,
, 的直角坐标方程;(2)当
的直角坐标方程;(2)当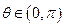 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.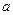
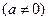 和
和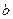 ,不等式
,不等式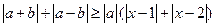 恒成立,试求实数
恒成立,试求实数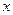 的取值范围.
的取值范围.C
[解析] 由基本不等式,得ab≤![]() =
=![]() =
=![]() -ab,所以ab≤
-ab,所以ab≤![]() ,故B错;
,故B错;![]() +
+![]() =
=![]() =
=![]() ≥4,故A错;由基本不等式得
≥4,故A错;由基本不等式得![]() ≤
≤![]() =
=![]() ,即
,即![]() +
+![]() ≤
≤![]() ,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×
,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×![]() =
=![]() ,故D错.故选C.
,故D错.故选C.
.定义域为R的函数 满足
满足 ,且当
,且当 时,
时, ,则当
,则当 时,
时, 的最小值为( )
的最小值为( )
(A) (B)
(B) (C)
(C) (D)
(D)
.过点 作圆
作圆 的弦,其中弦长为整数的共有 ( )
的弦,其中弦长为整数的共有 ( )
A.16条 B. 17条 C. 32条 D. 34条
一、选择题(每小题5分,满分60分)
1
2
3
4
5
6
7
8
9
10
11
12
D
C
D
B
B
A
C
C
A
D
A
D
二、填空题(每小题4分,满分16分)
13.-6 14. 15.
15. 16.②③
16.②③
三、解答题(第17、18、19、20、21题各12分,第22题14分,共74分)
17.(I)

(Ⅱ)



 函数
函数 的值域为
的值域为
18.解:(I)记“甲回答对这道题”、“乙回答对这道题”、“丙回答对这道题”分别为事件
 、
、 、
、 ,则
,则 ,且有
,且有 即
即

(Ⅱ)由(1)
则甲、乙、丙三人中恰有两人回答对该题的概率为:

19.解:法一
(I)设 是
是 的中点,连结
的中点,连结 ,
,
则四边形 为方形,
为方形, ,故
,故 ,
,

 即
即
又
 平面
平面
(Ⅱ)由(I)知 平面
平面 ,
,
又 平面
平面 ,
, ,
,
取 的中点
的中点 ,连结
,连结 又
又 ,
,
则 ,取
,取 的中点
的中点 ,连结
,连结 则
则
 为二面角
为二面角 的平面角
的平面角
连结 ,在
,在 中,
中, ,
,
取 的中点
的中点 ,连结
,连结 ,
, ,在
,在 中,
中,

 二面角
二面角 的余弦值为
的余弦值为
法二:
 (I)以
(I)以 为原点,
为原点, 所在直线分别为
所在直线分别为 轴,
轴, 轴,
轴, 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则


又因为
所以, 平面
平面
(Ⅱ)设 为平面
为平面 的一个法向量。
的一个法向量。
由 得
得
取 ,则
,则 又
又 ,
,
设 为平面
为平面 的一个法向量,由
的一个法向量,由 ,
, ,
,
得 取
取 取
取
设 与
与 的夹角为
的夹角为 ,二面角
,二面角 为
为 ,显然
,显然 为锐角,
为锐角,
 ,即为所求
,即为所求
20.解:(I) 或
或
故 的单调递增区间是
的单调递增区间是 和
和
单调递减区间是(0,2)
(Ⅱ)



 在
在 和
和 递增,在(-1,3)递减。
递增,在(-1,3)递减。
 有三个相异实根
有三个相异实根

21.解:(I)设 的公差为
的公差为 ,则:
,则:

(Ⅱ)当 时,
时, ,由
,由 ,得
,得
当 时,
时, ,
,
 ,即
,即
 是以
是以 为首项,
为首项, 为公比的等比数列。
为公比的等比数列。
(Ⅲ)由(Ⅱ)可知:


22.解:(I)设过 与抛物线
与抛物线 的相切的直线的斜率是
的相切的直线的斜率是 ,
,
则该切线的方程为:
由 得
得

则 都是方程
都是方程 的解,故
的解,故
(Ⅱ)设
由于 ,故切线
,故切线 的方程是:
的方程是:
则
 ,同理
,同理
则直线 的方程是
的方程是 ,则直线
,则直线 过定点(0,2)
过定点(0,2)
(Ⅲ)要使 最小,就是使得
最小,就是使得 到直线
到直线 的距离最小,而
的距离最小,而 到直线
到直线 的距离
的距离

当且仅当 即
即 时取等号
时取等号
设
由 得
得 ,则
,则



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com