
题目列表(包括答案和解析)
已知函数 ,若实数
,若实数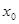 是函数
是函数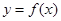 的零点,且
的零点,且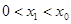 ,那么
,那么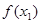 的值
( )
的值
( )
A.恒为正值 B.等于0 C.恒为负值 D.不大于0
已知函数![]() ,若实数
,若实数![]() 是函数
是函数![]() 的零点,且
的零点,且![]() ,
,
那么![]() 的值 ( )
的值 ( )
A.恒为正值 B.等于0 C.恒为负值 D.不大于0
设有两个命题,命题p:关于x的不等式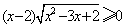 的
的
解集为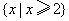 ,命题q:若函数
,命题q:若函数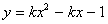 的值恒小
的值恒小
于0,则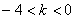 ,那么
,那么
A.“p且q”为真命题 B.“p或q”为真命题
C. “﹁p”为真命题 D. “﹁q”为假命题
对于函数![]() ,如果存在实数
,如果存在实数![]() 使得
使得![]() ,那么称
,那么称![]() 为
为![]() 的生成函数.
的生成函数.
(1)下面给出两组函数,![]() 是否分别为
是否分别为![]() 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组:![]() ;
;
第二组:![]() ;
;
(2)设![]() ,生成函数
,生成函数![]() .若不等式
.若不等式
![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,取
,取![]() ,生成函数
,生成函数![]() 图像的最低点坐标为
图像的最低点坐标为![]() .若对于任意正实数
.若对于任意正实数![]() 且
且![]() .试问是否存在最大的常数
.试问是否存在最大的常数![]() ,使
,使![]() 恒成立?如果存在,求出这个
恒成立?如果存在,求出这个![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
已知函数![]() 在区间
在区间![]() 上均有意义,且
上均有意义,且![]() 、
、![]() 是其图象上横坐标分别为
是其图象上横坐标分别为![]() 、
、![]() 的两点.对应于区间
的两点.对应于区间![]() 内的实数
内的实数![]() ,取函数
,取函数![]() 的图象上横坐标为
的图象上横坐标为![]() 的点
的点![]() ,和坐标平面上满足
,和坐标平面上满足![]() 的点
的点![]() ,得
,得![]() .对于实数
.对于实数![]() ,如果不等式
,如果不等式![]() 对
对![]() 恒成立,那么就称函数
恒成立,那么就称函数![]() 在
在![]() 上“k阶线性近似”.若函数
上“k阶线性近似”.若函数![]() 在
在![]() 上“k阶线性近似”,则实数k的取值范围为
上“k阶线性近似”,则实数k的取值范围为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
1.B 2.A 3.C 4.B 5.A 6.B 7.D 8.C 9.C 1 0.B
11.B 12.D
【解析】
1. .
.
2. .
.
3. 是方程
是方程 的根,
的根, 或8,又
或8,又 ,
,
 .
.
4. .
.
5.画出可行域,如图, 可看为区域内的点与(0,0)连线的斜率,
可看为区域内的点与(0,0)连线的斜率, .
.
 .
.
6.


7.连 ,设
,设
 平面
平面 .
.
 是
是 与平面
与平面 所成的角.
所成的角.  ,
,
 .
.
8.据 的图象知
的图象知  的解集为
的解集为 .
.
9.由 知
知 点的轨迹是以
点的轨迹是以 ,
, 为焦点的双曲线一支.
为焦点的双曲线一支. ,
, .
.
10.将命中连在一起的3枪看作一个整体和另外一枪命中的插入没有命中的4枪留下的5个空档,故有 种.
种.
11.设 ,圆为
,圆为 最长弦
最长弦 为直径,最短弦
为直径,最短弦 的中点为
的中点为 ,
,


12.几何体的表面积是三个圆心角为 、半径为1的扇形面积与半径为1的球面积的
、半径为1的扇形面积与半径为1的球面积的 之和,即表面积为
之和,即表面积为 .
.
二、
13.
 平方得
平方得
 .
.
14.55 

 .
.
15.1  与
与 互为反函数,
互为反函数,
 ,
,
 .
.
16. 或
或
 ,设
,设
 或
或 .
.
三、解答题
17.(1) 的最大值为2,
的最大值为2, 的图象经过点
的图象经过点
 ,
, ,
, ,
,

 .
.
(2) ,
,


 .
.
18.(1)∵当 时,
时, 总成等差数列,
总成等差数列,

即 ,所以对
,所以对 时,此式也成立
时,此式也成立
 ,又
,又 ,两式相减,
,两式相减,
得 ,
,
 成等比数列,
成等比数列, .
.
(2)由(1)得

 .
.
19.(1)由题意知,袋中黑球的个数为
记“从袋中任意摸出2个球,得到的都是黑球”为事件 ,则
,则 .
.
(2)记“从袋中任意摸出2个球,至少得到一个白球”为事件 ,设袋中白球的个数为
,设袋中白球的个数为 ,则
,则 .
. 或
或 (含).
(含). .∴袋中白球的个数为5.
.∴袋中白球的个数为5.
20.(1)证明: .
.
连接 .
.
 ,又
,又

即
 平面
平面 .
.
(2)方法1 取 的中点
的中点 ,
, 的中点
的中点 ,
, 为
为 的中点,
的中点, 或其补角是
或其补角是 与
与 所成的角,连接
所成的角,连接 是
是 斜边
斜边 上的中线,
上的中线, ,
,
 .
.
在 中,由余弦定理得
中,由余弦定理得 ,
,
∴直线 与
与 所成的角为
所成的角为 .
.
(方法2)如图建立空间直角坐标系 .
.
则

 .
.
 .
.
∴直线 与
与 所成的角为
所成的角为 .
.
(3)(方法l)
 平面
平面 ,过
,过 作
作 于
于 ,由三垂线定理得
,由三垂线定理得 .
.
 是二面角
是二面角 的平面角,
的平面角,
 ,又
,又 .
.
在 中,
中, ,
, .
.
∴二面角 为
为 .
.
(方法2)
在上面的坐标系中,平面 的法向量
的法向量 .
.
设平面 的法向量
的法向量 ,则
,则 ,
,
解得

 ,
, .
.
∴二面角 为
为 .
.
21.(1)
 的最小值为
的最小值为 ,
, ,又直线
,又直线 的斜率为
的斜率为 .
.
 ,故
,故 .
.
(2) ,当
,当 变化时,
变化时, 、
、 的变化情况如下表:
的变化情况如下表:








0

0


ㄊ
极大
ㄋ
极小
ㄊ
∴函数 的单调递增区间是
的单调递增区间是 和
和
 ,
,
∴当 时,
时, 取得最小值
取得最小值 ,
,
当 时,
时, 取得最大值18.
取得最大值18.
21.(1)设 .
.
由抛物线定义, ,
,  .
.
 在
在 上,
上, ,又
,又

 或
或 舍去.
舍去.

∴椭圆 的方程为
的方程为 .
.
(2)① 直线 的方程为
的方程为
 为菱形,
为菱形, ,设直线
,设直线 的方程为
的方程为
由 ,得
,得
 、
、 在椭圆
在椭圆 上,
上, 解得
解得 ,设
,设 ,则
,则 ,
, 的中点坐标为
的中点坐标为 .
.
由 为菱形可知,点
为菱形可知,点 在直线
在直线 上,
上,
 .
.
∴直线 的方程为
的方程为 即
即 .
.
② ∵ 为菱形,且
为菱形,且 ,
,
 ,∴菱形
,∴菱形 的面积
的面积


 .
.
∴当 时,菱形
时,菱形 的面积取得最大值
的面积取得最大值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com