题目列表(包括答案和解析)
(l3分)已知数列
满足递推关系式：
，且
．
(1)求
的取值范围；
(2)用数学归纳法证明：
；
，求证：
．| 2 |
| 1 |
| 2n |
| 1 |
| an |
| 2 |
| 12 |
| 2n |
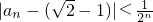（n≥3，n∈N）；
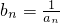，求证：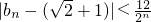
（n≥3，n∈N）．一、选择题：1―5 BDACB 6―12ABACＡ ＣB
二、填空题13．2 14．
15．
16．①⑧⑤ 或①③⑧ 或④⑧①或④①⑧
17.（1）解：在
中 
2分
4分
…….6分
（2）
10分
18．解：（1）在正方体
中，
、
、
、
分别为
、
、
、
中点
即
平面
到平面的距离即
到平面的距离． 3分
在平面
中，连结
则
故到
之距为
因此到平面的距离为
……………6分
（2）在四面体
中，
又底面三角形
是正三角形，
：
设到之距为
故
与平面所成角
的正
…………12分
另解向量法
19．解：（Ⅰ）设
、
两项技术指标达标的概率分别为
、
由题意得：
…………..…………..4分
解得：
或
，∴
. 即，一个零件经过检测为合格品的概率为
. ………. ……………………………….8分
（Ⅱ）任意抽出5个零件进行检查，其中至多3个零件是合格品的概率为
………………..12分
20．解：（1）
又
………………4分
（2）由
知
…………8分
（3）
21.解：（1）
2分
-1
（x）
-
0
+
0
-
（x）
减
极小值0
增
极大值
减
6分
（2）
8分
………….12分
22.解法一：（Ⅰ）设点
，则
，由
得：
，化简得
．……………….3分
（Ⅱ）（1）设直线
的方程为：
．
设
，
，又
，
联立方程组
，消去得：
，
，
……………………………………6分
由
，
得：
，
，整理得：
，
，
．……………………………………………………………9分
解法二：（Ⅰ）由得：
，
，
，
．
所以点的轨迹
是抛物线，由题意，轨迹的方程为：
．
（Ⅱ）（1）由已知，，得
．
则：
．…………①
过点
分别作准线
的垂线，垂足分别为
，
，
则有：
．…………②
，．
所以点的轨迹是抛物线，由题意，轨迹的方程为：．
（Ⅱ）（1）由已知，，得．
则：．…………①
过点分别作准线的垂线，垂足分别为，，
则有：．…………②
由①②得：
，即
．
（Ⅱ）（2）解：由解法一，
．
当且仅当
，即
时等号成立，所以
最小值为
．…………..12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com