练习册

  • 练习册
  • 试题
    C．2.7,78 D．2.7,83 【查看更多】

     

    题目列表(包括答案和解析)

    设集合S={1，2，3，4，5，6，7，8，9}，集合A={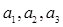 }是S的子集，且 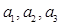满足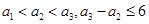，那么满足条件的集合A的个数为（    ）

    A．78                       B．76                        C．84                       D．83

     

    查看答案和解析>>

    某学校课题组为了研究学生的数学成绩和物理成绩之间的关系，随机抽取高二年级20名学生某次考试成绩(百分制)如下表所示：

    序号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    数学成绩

    95

    75

    80

    94

    92

    65

    67

    84

    98

    71

    物理成绩

    90

    63

    72

    87

    91

    71

    58

    82

    93

    81

     

    序号

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    数学成绩

    67

    93

    64

    78

    77

    90

    57

    83

    72

    83

    物理成绩

    77

    82

    48

    85

    69

    91

    61

    84

    78

    86

    某数学成绩90分(含90分)以上为优秀，物理成绩85分(含85分)以上为优秀．

    有多少的把握认为学生的数学成绩与物理成绩之间有关系（     ）

            A. 99.9%           B. 99%          C. 97.5%          D. 95%

     

    查看答案和解析>>

    某学校课题组为了研究学生的数学成绩和物理成绩之间的关系，随机抽取高二年级20名学生某次考试成绩(百分制)如下表所示：

    序号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    数学成绩

    95

    75

    80

    94

    92

    65

    67

    84

    98

    71

    物理成绩

    90

    63

    72

    87

    91

    71

    58

    82

    93

    81

    序号

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    数学成绩

    67

    93

    64

    78

    77

    90

    57

    83

    72

    83

    物理成绩

    77

    82

    48

    85

    69

    91

    61

    84

    78

    86

    某数学成绩90分(含90分)以上为优秀，物理成绩85分(含85分)以上为优秀．有多少的把握认为学生的数学成绩与物理成绩之间有关系（　　 ）　

    　　　 A. 99.9%　 　　　　B. 99%　　　　 C. 97.5%　　　　 D. 95%

    查看答案和解析>>

    某学校课题组为了研究学生的数学成绩与物理成绩之间的关系，随机抽取高二年级20名学生某次考试成绩（满分100分）如下表所示：
    序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
    数学成绩 95 75 80 94 92 65 67 84 98 71 67 93 64 78 77 90 57 83 72 83
    物理成绩 90 63 72 87 91 71 58 82 93 81 77 82 48 85 69 91 61 84 78 86
    若单科成绩85分以上（含85分），则该科成绩为优秀．
    （1）根据上表完成下面的2×2列联表（单位：人）：
    数学成绩优秀 数学成绩不优秀   合   计
    物理成绩优秀
    物理成绩不优秀
    合   计 20
    （2）根据题（1）中表格的数据计算，有多大的把握，认为学生的数学成绩与物理成绩之间有关系？
    参考数据：
    ①假设有两个分类变量X和Y，它们的值域分别为{x1，x2}和y1，y2，其样本频数列联表（称为2×2列联表）为：
    y1 y2 合计
    x1 a b a+b
    x2 c d c+d
    合计 a+c b+d a+b+c+d
    则随机变量K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，其中n=a+b+c+d为样本容量；
    ②独立检验随机变量K2的临界值参考表：
    P（K2≥k0） 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
    k0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828

    查看答案和解析>>

    某学校课题组为了研究学生的数学成绩与物理成绩之间的关系，随机抽取高二年级20名学生某次考试成绩（满分100分）如下表所示：
    序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
    数学成绩 95 75 80 94 92 65 67 84 98 71 67 93 64 78 77 90 57 83 72 83
    物理成绩 90 63 72 87 91 71 58 82 93 81 77 82 48 85 69 91 61 84 78 86
    若单科成绩85分以上（含85分），则该科成绩为优秀．
    （1）根据上表完成下面的2×2列联表（单位：人）：
    数学成绩优秀 数学成绩不优秀   合   计
    物理成绩优秀
    物理成绩不优秀
    合   计 20
    （2）根据题（1）中表格的数据计算，有多大的把握，认为学生的数学成绩与物理成绩之间有关系？
    参考数据：
    ①假设有两个分类变量X和Y，它们的值域分别为{x1，x2}和y1，y2，其样本频数列联表（称为2×2列联表）为：
    y1 y2 合计
    x1 a b a+b
    x2 c d c+d
    合计 a+c b+d a+b+c+d
    则随机变量K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，其中n=a+b+c+d为样本容量；
    ②独立检验随机变量K2的临界值参考表：
    P（K2≥k0） 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
    k0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828

    查看答案和解析>>

     

    一、选择题

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    答案

    C

    C

    A

    C

    D

    D

    C

    B

    A

    B

     

    二、填空题

    11. ；        12. （或）;       13.  15;          14. 6;      

    15.              16. ；                     17.

    三、解答题

                                     …………12′

      故函数的取值范围是…………12′      

     

    19. 解：(1)设袋中原有n个白球,由题意知：，所以=12，

    解得n=4(舍去),即袋中原有4个白球;                          …………4′

    (2)由题意,的可能取值为1，2，3，4

    所以，取球次数的分布列为：

    1

    2

    3

    4

    P

                                                                 …………9′  

    (Ⅲ)因为甲先取,所以甲只有可能在第1次和第3次取球,记“甲取到白球”的事件为A，

    则或 “=3”）,所以  …………14′ 

    20. 解：⑴由条件得：  ∴     ∵ ∴ ∴为等比数列∴                                 …………4′

     ⑵由   得           

         又   ∴                                 …………9′  ⑶∵

    （或由即），∴为递增数列.                            

    ∴从而      

    ∴

                                             …………14′

    21.解：（1）依题意有，由显然，得，化简得；                                                    …………5′

    （2）证明：（?）

                                                …………10′

    （?）设点A、B的坐标分别为，不妨设点A在点P与点B之间，点，依（?）有*，又可设过点P（2,4）的直线方程为，得，

    ，代入上*式得

    ，又，得

     ，当直线AB的斜率不存在时，也满足上式.即点Q总过直线，得证.                                                               …………15′

    22. 解：（Ⅰ）设与在公共点处的切线相同．，，由题意，．即由得：，或（舍去）．即有．                              …………4′

    令，则．于是当，即时，；

    当，即时，．故在为增函数，在为减函数，于是在的最大值为．                    …………8′

    （Ⅱ）设

    则．故在为减函数，在为增函数，于是函数在上的最小值是．故当时，有，即当时，．       …………15′

     

     


    同步练习册答案