
题目列表(包括答案和解析)
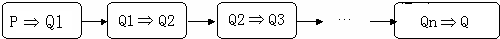
| A、P1=P2 | B、P1<P2 | C、P1>P2 | D、以上三种情况都有可能 |
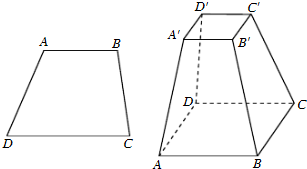 (必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.
(必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.| x |
| x+h |
| a |
| b |
| ah |
| b-a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| h |
| y-a |
| b-a |
| b-a |
| h |
| ∫ | h 0 |
| b-a |
| h |
| b-a |
| 2h |
| | | h 0 |
| b-a |
| 2h |
| 1 |
| 2 |
| 1 |
| 3 |

20.用循环语句描述1+ +
+ +
+ +…+
+…+ .
.
解:算法分析:
第一步是选择一个变量S表示和,并赋给初值0,再选取一个循环变量i,并赋值为0;
第二步开始进入WHILE循环语句,首先判断i是否小于9;
第三步为循环表达式(循环体),用WEND来控制循环;
第四步用END来结束程序.
可写出程序如下:
S=0
i=0
WHILE i<=9
S=S+1/2^i
i=i+1
WEND
PRINT S
END
运行该程序,输出:
S=1.9980
21.目前高中毕业会考中,成绩在85~100为“A”,70~84为“B”,60~69为“C”,60分以下为“D”.编制程序,输入学生的考试成绩(百分制,若有小数则四舍五入),输出相应的等级.
答案:
I=1
WHILE I=1
INPUT “shu ru xue sheng cheng ji a=”;a
IF a<60 THEN
PRINT “D”
ELSE
IF a<70 THEN
PRINT “C”
ELSE
IF a<85 THEN
PRINT “B”
ELSE
PRINT “A”
END IF
END IF
END IF
INPUT “INPUT 1,INPUT 2”;I
WEND
END
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com