
题目列表(包括答案和解析)
| x2+a |
| bx-c |
| 1 |
| 2 |
| 1 |
| an |
 (b,c∈N*),满足f(0)=0,f(2)=2,且f(-2)<
(b,c∈N*),满足f(0)=0,f(2)=2,且f(-2)< .
.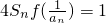 ,(Sn为该数列的前n项的和),如果存在,写出数列的一个通项公式an,并说明满足条件的数列{an}是否唯一确定;如果不存在,请说明理由.
,(Sn为该数列的前n项的和),如果存在,写出数列的一个通项公式an,并说明满足条件的数列{an}是否唯一确定;如果不存在,请说明理由.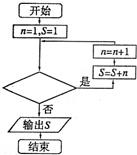 5、已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的种序框图计算该数列的第10项,则判断框内的条件是( )
5、已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的种序框图计算该数列的第10项,则判断框内的条件是( )| 1 |
| 2 |
| n |
 |
| i=1 |
| ai |
| i |
| 1 |
| 2 |
| 1 |
| 2n |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com