
题目列表(包括答案和解析)
已知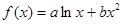 在点(1,f(1))处的切线方程为
在点(1,f(1))处的切线方程为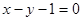 。
。
(1)求f(x)的表达式;
(2)若f(x)满足 恒成立,则称f(x)为g(x)的一个“上界函数”,如果f(x)为
恒成立,则称f(x)为g(x)的一个“上界函数”,如果f(x)为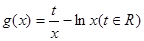 的一个“上界函数”,求t的取值范围;
的一个“上界函数”,求t的取值范围;
(3)当m>0时讨论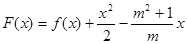 在区间(0,2)上极值点的个数。
在区间(0,2)上极值点的个数。
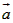 =(-1,x2+m),
=(-1,x2+m), =(m+1,
=(m+1, ),当m>0时,求使不等式
),当m>0时,求使不等式 >0成立的x的取值范围。
>0成立的x的取值范围。 设数列{an}的前n项和为Sn,且Sn=(m+1)-man![]() 对任意正整数n都成立,其中m为常数,且m<-1.
对任意正整数n都成立,其中m为常数,且m<-1.
(1)求证:{an}是等比数列;
(2)设数列{an}的公比q=f(m),数列{bn}满足:b1=![]() a1,bn=f(bn-1)(n≥2,n∈N*). 试问当m为何值时,
a1,bn=f(bn-1)(n≥2,n∈N*). 试问当m为何值时,![]() 成立?
成立?
当m>1时,关于x的不等式x2+(m-1)x-m≥0的解集是
A.{x|x≤1,或x≥-m} B. {x|1≤x≤-m }
C.{x|x≤-m,或x≥1} D. {x|-m≤x≤1 }
某同学在研究函数f(x)=x2ex的性质时,得到如下结论:
①f(x)的单调递增区间是(0,+∞);
②f(x)在x=0处取极小值,在x=-2处取极大值;
③f(x)有最小值,无最大值;
④f(x)的图象与它在(0,0)处的切线有两个交点;
⑤当m>1时,f(x)的图象与直线x=m只有一个交点.
其中正确结论的序号是 .
(把你认为正确结论的序号都填上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com