题目列表(包括答案和解析)
22-12=2×1+1,
32-22=2×2+1,
42-32=2×3+1,
……
(n+1)2-n2=2n+1.
将以上各等式两边分别相加得（n+1）2-12=2(1+2+…+n)+n,即1+2+3+…+n=
.
（1）类比上述求法，请你求出12+22+32+…+n2的值.
（2）根据上述结论试求12+32+52+…+992的值.?
22-12=2×1+1,
32-22=2×2+1,
42-32=2×3+1,
……
(n+1)2-n2=2n+1.
将以上各等式两边分别相加得（n+1）2-12=2(1+2+…+n)+n,即1+2+3+…+n=
.
（1）类比上述求法，请你求出12+22+32+…+n2的值.
（2）根据上述结论试求12+32+52+…+992的值.?
| n(n+1) | 2 |
通过计算可得下列等式：
┅┅
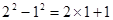
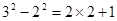
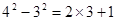
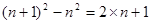
将以上各式分别相加得：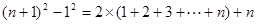
即：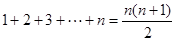
类比上述求法：请你求出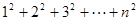
的值.
（本小题满分12分）
通过计算可得下列等式：
，
，
，┅┅，
将以上各式分别相加得：
即：
类比上述求法：请你求出
的值(要求必须有运算推理过程).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com