
题目列表(包括答案和解析)
已知 是公差为d的等差数列,
是公差为d的等差数列, 是公比为q的等比数列
是公比为q的等比数列
(Ⅰ)若  ,是否存在
,是否存在 ,有
,有 ?请说明理由;
?请说明理由;
(Ⅱ)若 (a、q为常数,且aq
(a、q为常数,且aq 0)对任意m存在k,有
0)对任意m存在k,有 ,试求a、q满足的充要条件;
,试求a、q满足的充要条件;
(Ⅲ)若 试确定所有的p,使数列
试确定所有的p,使数列 中存在某个连续p项的和式数列中
中存在某个连续p项的和式数列中 的一项,请证明.
的一项,请证明.
【解析】第一问中,由 得
得 ,整理后,可得
,整理后,可得
 、
、 ,
, 为整数
为整数 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)中当 时,则
时,则
 即
即 ,其中
,其中 是大于等于
是大于等于 的整数
的整数
反之当 时,其中
时,其中 是大于等于
是大于等于 的整数,则
的整数,则 ,
,
显然 ,其中
,其中

 、
、 满足的充要条件是
满足的充要条件是 ,其中
,其中 是大于等于
是大于等于 的整数
的整数
(3)中设 当
当 为偶数时,
为偶数时, 式左边为偶数,右边为奇数,
式左边为偶数,右边为奇数,
当 为偶数时,
为偶数时, 式不成立。由
式不成立。由 式得
式得 ,整理
,整理
当 时,符合题意。当
时,符合题意。当 ,
, 为奇数时,
为奇数时,
结合二项式定理得到结论。
解(1)由 得
得 ,整理后,可得
,整理后,可得
 、
、 ,
, 为整数
为整数 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)当 时,则
时,则
 即
即 ,其中
,其中 是大于等于
是大于等于 的整数反之当
的整数反之当 时,其中
时,其中 是大于等于
是大于等于 的整数,则
的整数,则 ,
,
显然 ,其中
,其中

 、
、 满足的充要条件是
满足的充要条件是 ,其中
,其中 是大于等于
是大于等于 的整数
的整数
(3)设 当
当 为偶数时,
为偶数时, 式左边为偶数,右边为奇数,
式左边为偶数,右边为奇数,
当 为偶数时,
为偶数时, 式不成立。由
式不成立。由 式得
式得 ,整理
,整理
当 时,符合题意。当
时,符合题意。当 ,
, 为奇数时,
为奇数时,

 由
由 ,得
,得

 当
当 为奇数时,此时,一定有
为奇数时,此时,一定有 和
和 使上式一定成立。
使上式一定成立。 当
当 为奇数时,命题都成立
为奇数时,命题都成立
已知 ,(其中
,(其中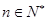 )
)
⑴求 及
及 ;
;
⑵试比较 与
与 的大小,并说明理由.
的大小,并说明理由.
【解析】第一问中取 ,则
,则 ;
…………1分
;
…………1分
对等式两边求导,得
取 ,则
,则 得到结论
得到结论
第二问中,要比较 与
与 的大小,即比较:
的大小,即比较: 与
与 的大小,归纳猜想可得结论当
的大小,归纳猜想可得结论当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
;
猜想:当 时,
时, 运用数学归纳法证明即可。
运用数学归纳法证明即可。
解:⑴取 ,则
,则 ;
…………1分
;
…………1分
对等式两边求导,得 ,
,
取 ,则
,则 。 …………4分
。 …………4分
⑵要比较 与
与 的大小,即比较:
的大小,即比较: 与
与 的大小,
的大小,
当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
…………6分
;
…………6分
猜想:当 时,
时, ,下面用数学归纳法证明:
,下面用数学归纳法证明:
由上述过程可知, 时结论成立,
时结论成立,
假设当 时结论成立,即
时结论成立,即 ,
,
当 时,
时,
而
∴
即 时结论也成立,
时结论也成立,
∴当 时,
时, 成立。
…………11分
成立。
…………11分
综上得,当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时,
 ,当且仅当
,当且仅当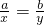 时,上式取等号,利用以上结论,可以得到函数
时,上式取等号,利用以上结论,可以得到函数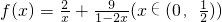 的最小值为
的最小值为数列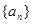 ,满足
,满足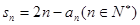
(1)求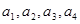 ,并猜想通项公式
,并猜想通项公式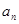 。
。
(2)用数学归纳法证明(1)中的猜想。
【解析】本试题主要考查了数列的通项公式求解,并用数学归纳法加以证明。第一问利用递推关系式得到 ,
,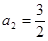 ,
,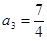 ,
,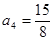 ,并猜想通项公式
,并猜想通项公式
第二问中,用数学归纳法证明(1)中的猜想。
①对n=1, 等式成立。
等式成立。
②假设n=k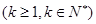 时,
时,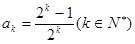 成立,
成立,
那么当n=k+1时,
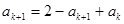 ,所以当n=k+1时结论成立可证。
,所以当n=k+1时结论成立可证。
数列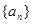 ,满足
,满足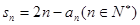
(1) ,
,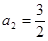 ,
,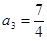 ,
,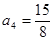 并猜想通项公
并猜想通项公 。 …4分
。 …4分
(2)用数学归纳法证明(1)中的猜想。①对n=1, 等式成立。 …5分
等式成立。 …5分
②假设n=k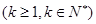 时,
时,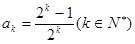 成立,
成立,
那么当n=k+1时,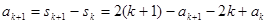
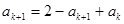 ,
……9分
,
……9分
所以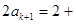
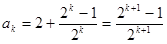
所以当n=k+1时结论成立 ……11分
由①②知,猜想对一切自然数n 均成立
均成立
已知点 为圆
为圆 上的动点,且
上的动点,且 不在
不在 轴上,
轴上, 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 交于
交于 、
、 两点。
两点。
(I)求曲线 的方程;
的方程;
(II)试证明:在 轴上存在定点
轴上存在定点 ,使得
,使得 总能被
总能被 轴平分
轴平分
【解析】第一问中设 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,
∴ ,曲线
,曲线 的方程为
的方程为
第二问中,设点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 , ………………3分
, ………………3分
代入曲线 的方程
的方程 ,可得
,可得 
∵ ,∴
,∴
确定结论直线 与曲线
与曲线 总有两个公共点.
总有两个公共点.
然后设点 ,
, 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
,
要使 被
被 轴平分,只要
轴平分,只要 得到。
得到。
(1)设 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,
∴ ,曲线
,曲线 的方程为
的方程为 . ………………2分
. ………………2分
(2)设点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 , ………………3分
, ………………3分
代入曲线 的方程
的方程 ,可得
,可得  ,……5分
,……5分
∵ ,∴
,∴ ,
,
∴直线 与曲线
与曲线 总有两个公共点.(也可根据点M在椭圆
总有两个公共点.(也可根据点M在椭圆 的内部得到此结论)
的内部得到此结论)
………………6分
设点 ,
, 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
,
要使 被
被 轴平分,只要
轴平分,只要 ,
………………9分
,
………………9分
即 ,
, , ………………10分
, ………………10分
也就是 ,
, ,
,
即 ,即只要
,即只要 ………………12分
………………12分
当 时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而 总能被
总能被 轴平分.
轴平分.
所以在x轴上存在定点 ,使得
,使得 总能被
总能被 轴平分
轴平分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com