
题目列表(包括答案和解析)
已知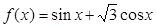 (
(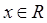 ).求:
).求:
(1)若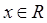 ,求
,求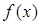 的值域,并写出
的值域,并写出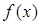 的单调递增区间;
的单调递增区间;
(2)若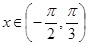 ,求
,求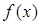 的值域.
的值域.
已知定义在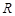 上的函数
上的函数 是偶函数,且
是偶函数,且 时,
时, 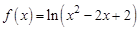 ,
,
(1)求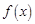 解析式; (2)写出
解析式; (2)写出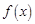 的单调递增区间。(本题满分12分)
的单调递增区间。(本题满分12分)
(12分)已知函数
(1)在给定的直角坐标系内画出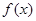 的图象;
的图象;
(2)写出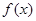 的单调递增区间(不需要证明);
的单调递增区间(不需要证明);
(3)写出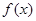 的最大值和最小值(不需要证明).
的最大值和最小值(不需要证明).
已知定义在 上的函数
上的函数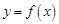 是偶函数,且
是偶函数,且 时,
时,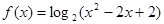 ,
,
[1].当 时,求
时,求 解析式;
解析式;
[2]写出 的单调递增区间。
的单调递增区间。
已知函数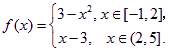
(1)在图5给定的直角坐标系内画出![]() 的图象;
的图象;
(2)写出![]() 的单调递增区间.
的单调递增区间.
1、A 2,、B 3、 D 4,、B 5、 D 6、C 7、A 8、B 9、A 10、D
11、(,1] 12、-或1 13、6p 14、2 15、11
16解:解:(Ⅰ)



当 ,即
,即
 时,
时, 取得最大值
取得最大值 .
.
(Ⅱ)当 ,即
,即
 时,
时,
所以函数 的单调递增区间是
的单调递增区间是

17、解:(Ⅰ)从15名教师中随机选出2名共 种选法, …………………………2分
种选法, …………………………2分
所以这2人恰好是教不同版本的男教师的概率是 . …………………5分
. …………………5分
(Ⅱ)由题意得
 ;
;  ;
; .
.
故 的分布列为
的分布列为

0
1
2





所以,数学期望 .
.
18、解法一:(Ⅰ)证明:连接





 ∥
∥ 。 ……………………3分
。 ……………………3分

 ∥平面
∥平面 …………………………5分
…………………………5分
(Ⅱ)解:在平面



 ―
― ―
― ……………………8分
……………………8分
设 。
。
在
所以,二面角 ―
― ―
― 的大小为
的大小为 。 ………………12分
。 ………………12分
19、(I)解:当
①当 , 方程化为
, 方程化为

②当 , 方程化为1+2x
= 0, 解得
, 方程化为1+2x
= 0, 解得 ,
,
由①②得, 
(II)解:不妨设 ,
,
因为
所以 是单调递函数, 故
是单调递函数, 故 上至多一个解,
上至多一个解,

20、解:(Ⅰ)由
 知,点
知,点 的轨迹
的轨迹 是以
是以 、
、 为焦点的双曲线右支,由
为焦点的双曲线右支,由 ,∴
,∴ ,故轨迹E的方程为
,故轨迹E的方程为 …(3分)
…(3分)
(Ⅱ)当直线l的斜率存在时,设直线l方程为 ,与双曲线方程联立消
,与双曲线方程联立消 得
得 ,设
,设 、
、 ,
,
|