
题目列表(包括答案和解析)
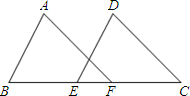 如图,点E、F是BC上的两点,AB∥DE,AB=DE,BE=CF.
如图,点E、F是BC上的两点,AB∥DE,AB=DE,BE=CF. 如图,点E、F是BC上的两点,AB∥DE,AB=DE,BE=CF.
如图,点E、F是BC上的两点,AB∥DE,AB=DE,BE=CF. 如图,已知点A、点B是直线上的两点,AB=12厘米,点C在线段AB上.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.
如图,已知点A、点B是直线上的两点,AB=12厘米,点C在线段AB上.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.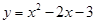 与x轴交于点A和点B,与y轴相交于点C.
与x轴交于点A和点B,与y轴相交于点C.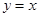 上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.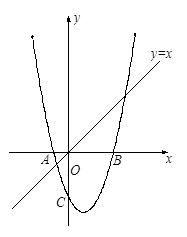
如图1,已知抛物线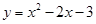 与x轴交于点A和点B,与y轴相交于点C.
与x轴交于点A和点B,与y轴相交于点C.
【小题1】求A、B、C三点的坐标
【小题2】点D为射线CB上的一动点(点D、B不重合),过点B作x轴的垂线BE与以点D为顶点的抛物线y=(x-t)2+h相交于点E,从△ADE和△ADB中任选一个三角形,求出当其面积等于△ABE的面积时的t的值;(友情提示:1、只选取一个三角形求解即可;2、若对两个三角形都作了解答,只按第一个解答给分.)
【小题3】如图2,若点P是直线 上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.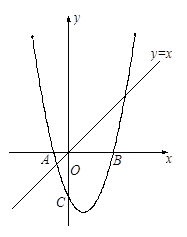
一、选择题
1. C 2. A 3.B 4.C 5.B 6.C 7.D 8.D 9.C 10.B
二、填空题
11. %20.files/image288.gif) ,
,%20.files/image290.gif) 12.
12. %20.files/image292.gif) 13.30º 14.
0.18;
13.30º 14.
0.18;
15. -7
16. (1)%20.files/image294.gif) ; (2)50。
; (2)50。
三、解答题
17.%20.files/image296.gif)
%20.files/image298.gif)
%20.files/image300.gif)
%20.files/image302.jpg) |
19.解:(1)%20.files/image304.gif) ,
,%20.files/image306.gif) ,同理
,同理%20.files/image308.gif)
%20.files/image310.gif)
%20.files/image312.gif)
%20.files/image314.gif)
(2)若%20.files/image316.gif) 平分
平分%20.files/image318.gif) ,四边形
,四边形%20.files/image320.gif) 是菱形.
是菱形.
证明:%20.files/image322.gif)
%20.files/image324.gif) ,
,%20.files/image326.gif)
%20.files/image328.gif) 四边形
四边形%20.files/image320.gif) 是平行四边形,
是平行四边形,%20.files/image331.gif)
%20.files/image333.gif)
%20.files/image328.gif) 平行四边形
平行四边形%20.files/image320.gif) 为菱形
为菱形
20.解:(1)(每图2分)………………………………………………………………4分
%20.files/image337.gif)
%20.files/image338.gif)
%20.files/image340.gif)
%20.files/image341.gif)
(2)0.12,36°;10,90°;(每空0.5分)…………………………………………………6分
(3)当旋钮开到36°附近时最省气,当旋钮开到90°时最省时.最省时和最省气不可能同时做到.………………………………………………………………………………………8分
说明:第(3)问只要表达意思明确即可,方式和文字不一定如此表达.
%20.files/image343.gif) |
%20.files/image345.gif) =0.4).
=0.4).21.
22.解:(2)%20.files/image347.gif) .???????????????????????????????????????????????????????????????????????????????????????????? 2分
.???????????????????????????????????????????????????????????????????????????????????????????? 2分
(3)如图③,当%20.files/image193.gif) 时,设
时,设%20.files/image158.gif) 切
切%20.files/image351.gif) 于点
于点%20.files/image162.gif) ,连结
,连结%20.files/image354.gif) ,
,
%20.files/image166.gif) ,
,%20.files/image357.gif) ,
,
%20.files/image358.gif)
%20.files/image360.gif) ,
,%20.files/image179.gif) ,????????????????????????????? 3分
,????????????????????????????? 3分
%20.files/image363.gif) ,
,%20.files/image365.gif) ,???????????????????????????? 4分
,???????????????????????????? 4分
%20.files/image367.gif) ,???????????????????????????? 5分
,???????????????????????????? 5分
%20.files/image369.gif) .?????????????????????????????????? 6分
.?????????????????????????????????? 6分
(4)%20.files/image371.gif) .????????????????????????????????????????????????????????????????????????????????????????????????? 8分
.????????????????????????????????????????????????????????????????????????????????????????????????? 8分
23.证明:(1)%20.files/image373.gif) ,
,%20.files/image375.gif)
%20.files/image377.gif) (2分)
(2分)
%20.files/image377.gif)
%20.files/image380.gif) (3分)
(3分)
(2)连结%20.files/image382.gif) (1分)
(1分) %20.files/image384.gif)
%20.files/image386.gif)
%20.files/image388.gif) (4分)
(4分)
%20.files/image390.gif)
%20.files/image392.gif)
%20.files/image394.gif)
%20.files/image396.gif)
%20.files/image398.gif) (5分)
(5分)
%20.files/image400.gif)
%20.files/image402.gif) (6分)
(6分)
%20.files/image404.gif)
%20.files/image406.gif) (7分)
(7分)
%20.files/image408.gif)
%20.files/image410.gif) (8分)
(8分)
24.解:(1)依题可得BP=t,CQ=2t,PC=t-2. ……………1分
∵EC∥AB,∴△PCE∽△PAB,%20.files/image412.gif) =
=%20.files/image414.gif) ,
,
∴EC=%20.files/image416.gif) .
……………3分
.
……………3分
QE=QC-EC=2t-%20.files/image416.gif) =
=%20.files/image419.gif) .
……………4分
.
……………4分
作PF⊥%20.files/image231.gif) ,垂足为F. 则PF=PB?sin60°=
,垂足为F. 则PF=PB?sin60°=%20.files/image422.gif) t
……………5分
t
……………5分
∴S=%20.files/image424.gif) QE?PF=
QE?PF=%20.files/image424.gif) ?
?%20.files/image419.gif) ?
?%20.files/image422.gif) t=
t=%20.files/image422.gif) (t2-2t+4)(t>2).
……6分
(t2-2t+4)(t>2).
……6分
(2)此时,C为PB中点,则t-2=2,∴=4. ……………8分
∴QE=%20.files/image419.gif) =
=%20.files/image431.gif) =6(厘米). ……………10分
=6(厘米). ……………10分
25.(1)∵点A的坐标为(0,16),且AB∥x轴
∴B点纵坐标为16,且B点在抛物线%20.files/image433.gif) 上
上
∴点B的坐标为(10,16)...............................1分
又∵点D、C在抛物线%20.files/image433.gif) 上,且CD∥x轴
上,且CD∥x轴
∴D、C两点关于y轴对称
∴DN=CN=5...............................2分
∴D点的坐标为(-5,4)...............................3分
(2)设E点的坐标为(a,16),则直线OE的解析式为:%20.files/image435.gif) ..........................4分
..........................4分
∴F点的坐标为(%20.files/image437.gif) )..............................5分
)..............................5分
由AE=a,DF=%20.files/image439.gif) 且
且%20.files/image441.gif) ,得
,得
%20.files/image443.gif) ..............................7分
..............................7分
解得a=5..............................8分
(3)连结PH,PM,PK
∵⊙P是△AND的内切圆,H,M,K为切点
∴PH⊥AD PM⊥DN PK⊥AN..............................9分
在Rt△AND中,由DN=5,AN=12,得AD=13
设⊙P的半径为r,则%20.files/image445.gif)
所以 r=2.............................11分
在正方形PMNK中,PM=MN=2
∴%20.files/image447.gif)
在Rt△PMF中,tan∠PFM=%20.files/image449.gif) .............................12分
.............................12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com