
题目列表(包括答案和解析)
| π | 2 |
(本题满分12分)已知函数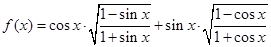
(1)求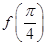 的值;(2)写出函数在
的值;(2)写出函数在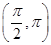 上的单调区间和值域。
上的单调区间和值域。
(本题满分12分)
已知函数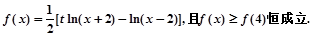
(1)求t的值;
(2)求x为何值时,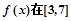 上取得最大值;
上取得最大值;
(3)设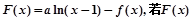 是单调递增函数,求a的取值范围.
是单调递增函数,求a的取值范围.
(本题满分12分)已知函数 ,
,
其中( 且
且
⑴求函数 的定义域;
的定义域;
⑵判断函数 的奇偶性,并予以证明;
的奇偶性,并予以证明;
⑶判断它在区间(0,1)上的单调性并说明理由。
(本题满分12分) 已知函数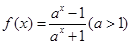 .
.
(1)判断函数的奇偶性;
(2)求该函数的值域;
(3)证明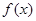 是
是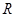 上的增函数.
上的增函数.
一、选择题
D A A C D C D C B B
二、填空题:
11.  12.
12. 13.81 14.
13.81 14. 15.②③
15.②③
三、解答题:
16.解:把函数 按向量
按向量
 平移后得
平移后得 ..............2分
..............2分
(Ⅰ) =
= ..................3分
..................3分
 ............5分
............5分
则函数 的值域为
的值域为 ;.....................7分
;.....................7分
(Ⅱ)当 时,
时, ,
,
 .............................................9分
.............................................9分
 恒有解,
恒有解, ,..................................11分
,..................................11分
即 ....................................................12分
....................................................12分
17.解:(Ⅰ)设三角形三内角A、B、C对应的三边分别为a, b, c,
∵ ,∴
,∴ ,由正弦定理有
,由正弦定理有 ,
,
又由余弦定理有 ,∴
,∴ ,即
,即 ,
,
所以 为Rt
为Rt ,且
,且 .................................. 3分
.................................. 3分
又

(1)÷(2),得 ...................................... 4分
...................................... 4分
令a=4k, b=3k (k>0)
则 ∴三边长分别为3,4,5.....................6分
∴三边长分别为3,4,5.....................6分
(Ⅱ)以C为坐标原点,射线CA为x轴正半轴建立直角坐标系,则A、B坐标为(3,0),(0,4),直线AB方程为
设P点坐标为(x, y),则由P到三边AB、BC、AB的距离为d1, d2和d3可知
 ,..................................8分
,..................................8分
且 故
故 .......................10分
.......................10分
令 ,由线性规划知识可知0≤m≤8,故d1+d2+d3的取值范围是
,由线性规划知识可知0≤m≤8,故d1+d2+d3的取值范围是 ......12分
......12分
18.解:(Ⅰ)当
 ………………2分
………………2分

 ,..............................................5分
,..............................................5分
故 ................6分
................6分
定义域为 .................................7分
.................................7分
(Ⅱ)对于 ,
,
显然当 (元), ..................................9分
(元), ..................................9分

∴当每辆自行车的日租金定在11元时,才能使一日的净收入最多。..........12分
19.解: (Ⅰ) ∵ (1)=0
(1)=0
∴(an+2-an+1)-(
即an+2-2an+1=2(an+1-2an)
又a2-
∴数列{an+1-2an}是以2为公比,以4为首项的等比数列。...............2分
∴an+1-2an=4×2n-1=2 n+1
∴ 且
且
∴数列{ }是首项为1,公差为1的等差数列,....................4分
}是首项为1,公差为1的等差数列,....................4分
∴ =
= +(n-1)×1=n
+(n-1)×1=n
∴ .....................................................6分
.....................................................6分
(Ⅱ)由 ,
,
令Sn=|b1|+|b2|+…+|bn|=+2()2+3()3+…+n()n
Sn=()2+2()3+…+(n-1)()n+n()n+1.......................8分
得Sn=+()2+()3+…+()n-n()n+1
=-n()n+1=2[1-()n]-n()n+1
∴ Sn=6[1-()n]-3n()n+1< .....................10分
.....................10分
要使得|b1|+|b2|+…+|bn|<m对于n∈N*恒成立,只须
所以实数 的取值范围是
的取值范围是 。.......................................12分
。.......................................12分
20.解:(Ⅰ)因为
又 是函数
是函数 的极值点,
的极值点, ,即
,即 ..............2分
..............2分
 ,则
,则
 ............4分
............4分
 .........................................................6分
.........................................................6分
(Ⅱ)由(Ⅰ)可知
故 .................................8分
.................................8分
令 ,当
,当 时,得
时,得 ,
,
则当 时,
时, ;当
;当 时,
时, ,
,
所以 在
在 上单调递减,在
上单调递减,在 单调递增,..................10分
单调递增,..................10分
故 时,
时, ,又
,又 ,..................................12分
,..................................12分
即对任意 ,恒有
,恒有 。..................................13分
。..................................13分
21.解:(Ⅰ) 以AB所在直线为x轴,线段AB的中垂线为y轴建立直角坐标系,
设 |CA|+|CB|=
所以焦距
因为 
又  ,所以
,所以  ,
,
由题意得  ...........................................4分
...........................................4分
此时,|PA|=|PB|,P点坐标为 P(0,±4).
所以C点的轨迹方程为  .............................6分
.............................6分
(Ⅱ)不妨设A点坐标为A(-3,0),M(x1,y1),N(x2,y2)
(1)当直线MN的倾斜角不为900时,设其方程为 y=k(x+3) 代入椭圆方程化简,得
 .......................................7分
.......................................7分
显然有
△≥0, 所以 
而由椭圆第二定义可得

......................... 10分
只要考虑
 的最小值,即考虑
的最小值,即考虑 取最小值,显然.
取最小值,显然.
当k=0时, 取最小值16. .................................12分
取最小值16. .................................12分
(2)当直线MN的倾斜角为900时,x1=x2=-3,得
 .....12分
.....12分
但  ,故
,故 ,这样的M、N不存在,即
,这样的M、N不存在,即 的最小值的集合为空集............................................................14分
的最小值的集合为空集............................................................14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com