练习册

  • 练习册
  • 试题
    已知函数. 【查看更多】

     

    题目列表(包括答案和解析)

    （本题满分15分）已知函数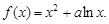

    （Ⅰ）当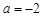时,求函数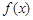的单调区间;

    （Ⅱ）若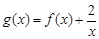在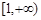是单调函数,求实数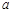的取值范围．

     

     

    查看答案和解析>>

    本题满分15分）已知函数（a-b）<b)。

    （I）当a=1，b=2时，求曲线在点（2，）处的切线方程。

    （II）设是的两个极值点，是的一个零点，且，

    证明：存在实数，使得 按某种顺序排列后的等差数列，并求

    查看答案和解析>>

    （本题满分15分）已知函数.

    (I)讨论在上的奇偶性；

    (II)当时，求函数在闭区间[-1,]上的最大值.

    查看答案和解析>>

    （本题满分15分）

    已知函数在[1，＋∞）上为增函数，且，

    （1）求的值；

    （2）若在[1，＋∞）上为单调函数，求实数的取值范围；

    （3）若在上至少存在一个，使得成立，求实数的取值范围．

     

    查看答案和解析>>

    （本题满分15分）

    已知函数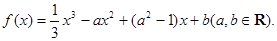

    （I）若x=1为的极值点，求a的值；

    （II）若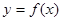的图象在点（1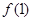，）处的切线方程为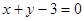，求在区间[-2，4]上的最大值；

    （III）当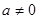时，若在区间（-1，1）上不单调，求a的取值范围.

     

    查看答案和解析>>

    2009.4

     

    1-10．CDABB   CDBDA

    11.       12. 4        13.        14.       15.  

    16.   17.

    18．解：（Ⅰ）由题意，有，

    ∴＝．…………………………5分

    由，得．

    ∴函数的单调增区间为 ．……………… 7分

    （Ⅱ）由，得．

    ∴．           ……………………………………………… 10分

    ∵，∴．      ……………………………………………… 14分

    19．解：（Ⅰ）设数列的公比为，由， 得.             …………………………………………………………… 4分

    ∴数列的通项公式为.      ………………………………… 6分

    （Ⅱ） ∵，    ，　　    ①

    .　 　   ②         

    ①－②得： …………………12分

                 得，                           …………………14分

    20.解：（I）取中点，连接.

    ∵分别是梯形和的中位线

    ∴，又

    ∴面面，又面

    ∴面.……………………… 7分

    （II）由三视图知，是等腰直角三角形，

         连接

         在面AC1上的射影就是，∴

         ，

    ∴当在的中点时，与平面所成的角

      是.           ………………………………14分

                                                   

    21．解：（Ⅰ）由题意：.

    为点M的轨迹方程.     ………………………………………… 4分

    （Ⅱ）由题易知直线l1，l2的斜率都存在，且不为0，不妨设，MN方程为与 联立得：，设6ec8aac122bd4f6e

        ∴由抛物线定义知：|MN|=|MF|+|NF|…………7分

           同理RQ的方程为，求得.  ………………………… 9分

    ∴．  ……………………………… 13分

    当且仅当时取“=”，故四边形MRNQ的面积的最小值为32．………… 15分

    22. 解：（Ⅰ），由题意得，

    所以                    ………………………………………………… 4分

    （Ⅱ）证明：令，，

    由得：，……………………………………………… 7分

    (1)当时，，在上，即在上单调递增，此时.

    ∴          …………………………………………………………… 10分

    (2)当时，，在上，在上，在 上，即在上单调递增，在上单调递减，在上单调递增，或者，此时只要或者即可，得或，

    ∴.                        …………………………………………14分

    由 (1) 、(2)得 .

    ∴综上所述，对于都，使得成立. ………………15分

     


    同步练习册答案