
题目列表(包括答案和解析)
(本小题满分15分)
设函数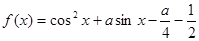 .
.
(1)当  ≤
≤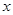 ≤
≤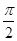 时,用
时,用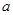 表示
表示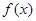 的最大值
的最大值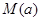 ;
;
(2)当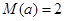 时,求
时,求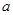 的值,并对此
的值,并对此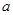 值求
值求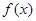 的最小值;
的最小值;
(3)问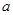 取何值时,方程
取何值时,方程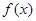 =
=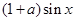 在
在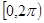 上有两解?
上有两解?
(本小题满分15分)如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,已知AB=a,AC=2,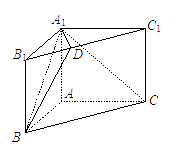 AA1=1,点D在棱B1C1上,且B1D∶DC1=1∶3.
AA1=1,点D在棱B1C1上,且B1D∶DC1=1∶3.
(Ⅰ)证明:BD⊥A1C;
(Ⅱ)若二面角B-A1D-B1的大小为60??,试求a的值.
(本小题满分15分)
已知函数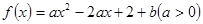 在区间
在区间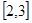 上的值域为
上的值域为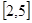
(1)求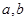 的值
的值
(2)若关于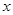 的函数
的函数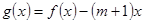 在
在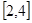 上为单调函数,求
上为单调函数,求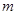 的取值范围
的取值范围
(本小题满分15分)如图,在四棱锥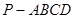 中,底面
中,底面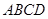 是正方形,侧棱
是正方形,侧棱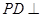 底面
底面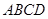 ,
,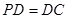 ,
,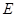 是
是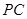 的中点,作
的中点,作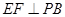 交
交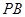 于点
于点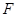
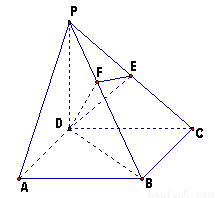
(1)证明: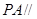 平面
平面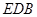 .
.
(2)证明: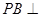 平面
平面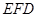 .
.
(3)求二面角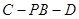 的大小.
的大小.
((本小题满分15分)
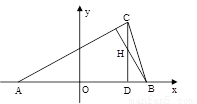
如图,在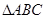 中,已知
中,已知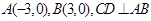 于
于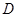 ,
,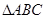 的垂心为
的垂心为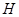 且
且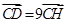 .
.
(Ⅰ)求点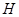 的轨迹方程;
的轨迹方程;
(Ⅱ)设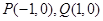 ,那么
,那么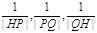 能否成等差数列?请说明理由;
能否成等差数列?请说明理由;
(Ⅲ)设直线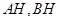 与直线
与直线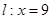 分别交于
分别交于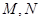 点,请问以
点,请问以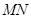 为直径的圆是否经过定点?并说明理由.
为直径的圆是否经过定点?并说明理由.
一、选择题:本大题共有10小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
D
A
A
C
B
B
B
C
D
A
二、填空题:本大题共有7小题,每小题4分,共28分.
11. .files/image283.gif) 12.
12..files/image285.gif) 13.
13..files/image287.gif) 14.
14..files/image289.gif)
15. .files/image291.gif) 16.
16. .files/image293.gif) 17.
17.
.files/image295.gif) 或
或.files/image297.gif)
三、解答题:本大题共5小题,共72分.解答应写出文字说明,证明过程或演算步骤.
18.解:(1)由正弦定理得:.files/image299.gif) .………………6分
.………………6分
(2).files/image301.gif)
.files/image186.gif) 的内角和
的内角和.files/image304.gif) ,
,.files/image188.gif)
.files/image307.gif)
.files/image309.gif) ………………8分
………………8分
.files/image311.gif) =
= .files/image313.gif)
.files/image315.gif)
.files/image317.gif) ………………10分
………………10分
.files/image319.gif) ,
,.files/image321.gif)
当.files/image323.gif) 即
即.files/image325.gif) 时,
时,.files/image194.gif) 取得最大值
取得最大值.files/image328.gif) .
………………14分
.
………………14分
19.(1)证明:连接.files/image198.gif) ,交
,交.files/image331.gif) 于
于.files/image333.gif) 点,连接
点,连接.files/image335.gif) ,得
,得.files/image335.gif) ∥
∥.files/image215.gif) ,
,
.files/image301.gif)
.files/image339.gif) 平面
平面.files/image217.gif) ,
,.files/image342.gif) 平面
平面.files/image217.gif) ,
,.files/image344.gif)
.files/image215.gif) //平面
//平面.files/image217.gif) . ………………7分
. ………………7分
(2) .files/image301.gif) 侧棱
侧棱.files/image207.gif) ⊥底面
⊥底面.files/image205.gif) ,
, .files/image344.gif)
.files/image207.gif) ⊥
⊥.files/image349.gif) ,过
,过.files/image220.gif) 作
作.files/image352.gif) ⊥
⊥.files/image349.gif) =
=.files/image355.gif) ,则
,则.files/image352.gif) ∥
∥.files/image207.gif) .
.
.files/image359.gif) ,
,.files/image344.gif)
.files/image361.gif) , ……12分
, ……12分
.files/image344.gif) 在棱
在棱.files/image213.gif) 上存在点
上存在点.files/image220.gif) 使三棱锥
使三棱锥.files/image365.gif) 的体积为
的体积为.files/image224.gif) ,且
,且.files/image220.gif) 是线段
是线段.files/image213.gif) 的三等分点.
的三等分点.
………………14分
20. 解:(1)由.files/image370.gif) ,得
,得.files/image372.gif) .
………………6分
.
………………6分
(2).files/image374.gif)
.files/image376.gif) ……………10分
……………10分
要使.files/image378.gif) 对
对.files/image246.gif) 成立,
成立,.files/image381.gif)
.files/image383.gif) ,故符合条件的正整数
,故符合条件的正整数.files/image385.gif) . ………………14分
. ………………14分
21.解:(1)设.files/image387.gif) ,则由
,则由.files/image389.gif) 得
得.files/image161.gif) 为
为.files/image392.gif) 中点,所以
中点,所以.files/image394.gif)
又.files/image396.gif) 得
得.files/image398.gif) ,
,.files/image400.gif) ,
,
所以.files/image402.gif) (
(.files/image404.gif) ).
………………6分
).
………………6分
(2)由(1)知.files/image249.gif) 为曲线
为曲线.files/image163.gif) 的焦点,由抛物线定义知,抛物线上任一点
的焦点,由抛物线定义知,抛物线上任一点.files/image408.gif) 到
到.files/image220.gif) 的距离等于其到准线的距离,即
的距离等于其到准线的距离,即.files/image411.gif) ,
,
所以.files/image413.gif) ,
,
根据.files/image263.gif) 成等差数列,得
成等差数列,得.files/image415.gif) , ………………10分
, ………………10分
直线.files/image265.gif) 的斜率为
的斜率为.files/image418.gif) ,
,
所以.files/image265.gif) 中垂线方程为
中垂线方程为.files/image420.gif) ,
………………12分
,
………………12分
又.files/image265.gif) 中点
中点.files/image422.gif) 在直线上,代入上式得
在直线上,代入上式得.files/image424.gif) ,即
,即.files/image426.gif) ,
,
所以点.files/image428.gif) .
………………15分
.
………………15分
22.解:(1)当.files/image430.gif) 时,
时,.files/image432.gif) 在区间
在区间.files/image028.gif) 上是增函数,
上是增函数,
当.files/image435.gif) 时,
时,.files/image437.gif) ,
,.files/image301.gif)
.files/image440.gif) ,
,.files/image442.gif)
.files/image344.gif) 函数
函数.files/image236.gif) 在区间
在区间.files/image028.gif) 上是增函数,
上是增函数,
综上得,函数.files/image236.gif) 在区间
在区间.files/image028.gif) 上是增函数.
………………7分
上是增函数.
………………7分
(2).files/image446.gif)
.files/image448.gif)
令.files/image450.gif) ………………10分
………………10分
设方程(*)的两个根为.files/image452.gif) (*)式得
(*)式得.files/image454.gif) ,不妨设
,不妨设.files/image456.gif) .
.
当.files/image458.gif) 时,
时,.files/image460.gif) 为极小值,所以
为极小值,所以.files/image462.gif) 在[0,1]上的最大值只能为
在[0,1]上的最大值只能为.files/image464.gif) 或
或.files/image466.gif) ;
;
………………10分
当.files/image468.gif) 时,由于
时,由于.files/image462.gif) 在[0,1]上是单调递减函数,所以最大值为
在[0,1]上是单调递减函数,所以最大值为.files/image464.gif) ,
,
所以在[0,1]上的最大值只能为.files/image464.gif) 或
或.files/image466.gif) ,
………………12分
,
………………12分
又已知.files/image462.gif) 在
在.files/image280.gif) 处取得最大值,所以
处取得最大值,所以.files/image472.gif)
即.files/image474.gif) . ………………15分
. ………………15分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com