
题目列表(包括答案和解析)
下面四个命题:
①在空间中,过直线外一点只能作一条直线与该直线平行;
②“直线 ⊥平面
⊥平面 内所有直线”的充要条件是“
内所有直线”的充要条件是“ ⊥平面
⊥平面 ”;
”;
③“平面 ∥平面
∥平面 ”的必要不充分条件是“
”的必要不充分条件是“ 内存在不共线三点到
内存在不共线三点到 的距离相等”;
的距离相等”;
④若 是异面直线,
是异面直线, 则
则 至少与
至少与 中的一条相交.
中的一条相交.
其中正确命题的个数有 ( )
A.1 B.2 C.3 D.4
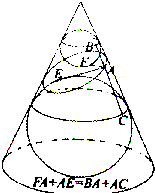 在空间中,取直线l为轴,直线l′与l相交于点O,其夹角为α(α为锐角),l′围绕l旋转得到以O为顶点,l′为母线的圆锥面,任取平面π,若它与轴l交角为β(π与l平行时,记β=0),则:当
在空间中,取直线l为轴,直线l′与l相交于点O,其夹角为α(α为锐角),l′围绕l旋转得到以O为顶点,l′为母线的圆锥面,任取平面π,若它与轴l交角为β(π与l平行时,记β=0),则:当 | π | 2 |
在空间中,取直线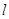 为轴,直线
为轴,直线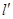 与
与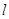 相交于点
相交于点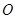 ,其夹角为
,其夹角为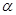 (
(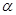 为锐角),
为锐角),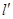 围绕
围绕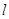 旋转得到以
旋转得到以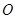 为顶点,
为顶点,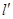 为母线的圆锥面,任取平面
为母线的圆锥面,任取平面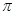 ,若它与轴
,若它与轴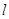 交角为
交角为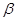 (
(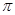 与
与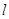 平行时,记
平行时,记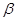 =0),则:当
=0),则:当 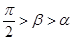 时,平面
时,平面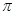 与圆锥面的交线为 .
与圆锥面的交线为 .
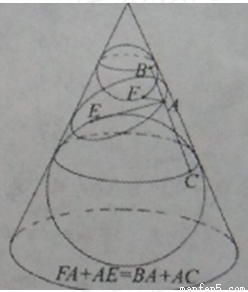
(1)β>α, __________________________;
(2)β=α, __________________________;
(3)β<α, __________________________.
| π |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com